保研机试复习

洛谷P2285 --[HNOI2004] 打鼹鼠

题目描述

鼹鼠是一种很喜欢挖洞的动物，但每过一定的时间，它还是喜欢把头探出到地面上来透透气的。根据这个特点阿牛编写了一个打鼹鼠的游戏：在一个 \(n \times n\) 的网格中，在某些时刻鼹鼠会在某一个网格探出头来透透气。你可以控制一个机器人来打鼹鼠，如果 \(i\) 时刻鼹鼠在某个网格中出现，而机器人也处于同一网格的话，那么这个鼹鼠就会被机器人打死。而机器人每一时刻只能够移动一格或停留在原地不动。机器人的移动是指从当前所处的网格移向相邻的网格，即从坐标为 \((i, j)\) 的网格移向 \((i-1, j), (i+1, j), (i, j-1), (i, j+1)\) 四个网格，机器人不能走出整个 \(n \times n\) 的网格。游戏开始时，你可以自由选定机器人的初始位置。

现在知道在一段时间内，鼹鼠出现的时间和地点，请编写一个程序使机器人在这一段时间内打死尽可能多的鼹鼠。

输入格式

第一行为 $n, m \(（\)n \(，\)m ^4\(），其中\)m$表示在这一段时间内出现的鼹鼠的个数，接下来的 \(m\) 行中每行有三个数据 \(\mathit{time}, x, y\) 表示在游戏开始后 \(\mathit{time}\) 个时刻，在第 \(x\) 行第 \(y\) 个网格里出现了一只鼹鼠。按递增的顺序给出。注意同一时刻可能出现多只鼹鼠，但同一时刻同一地点只可能出现一只鼹鼠。

输出格式

仅包含一个正整数，表示被打死鼹鼠的最大数目。

样例

样例输入

2 2	         
1 1 1		
2 2 2

样例输出

1

解题分析

最开始的时候我没有想到方法，因为有时间、坐标x和y，我想的是开三维数组解决，但是这样会爆时间。最后看了下别人的思路，个人感觉还是比较妙的。

因为输入数据每个时间点是递增的，那么我们就可以转变思路，用动态规划的思想来分析\({t}_i\)在时刻以\(({x}_i,{y}_i)\)为结束的击打序列中，最多击打数是多少。同时机器人移动只能在四方向移动，那么我们可以认为只要第\(i\)个鼹鼠与前\(i-1\)个鼹鼠之间的曼哈顿距离小于相距时间的话就可以依次打到，这样就可以构建状态转移方程 \[ dp[i] = \begin{cases}max(dp[i],dp[j]+1) & \ abs({x_i} - {y_i}) + abs({y}_i-{y}_j)\leqslant abs({t}_i-{t}_j) \\ 1& \ abs({x_i} - {y_i}) + abs({y}_i-{y}_j)\gt abs({t}_i-{t}_j)\end{cases} \]

代码

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
const int N=1e4+10;
typedef struct Node{
    int t,x,y;
}Node;
int dp[N];
int main(){
    int n,m;
    cin>>n>>m;
    Node node[N]; 
    for(int i = 0;i<m;i++) cin>>node[i].t>>node[i].x>>node[i].y;
    for(int i = 0;i<m;i++){
        dp[i] = 1;
        for(int j = 0;j < i ;j++){
            if(abs(node[i].x - node[j].x) + abs(node[i].y - node[j].y) <= abs(node[i].t - node[j].t))
                dp[i] = max(dp[i],dp[j] + 1);
        }
    }
    int res = 0;
    for(int i = 0;i<m;i++) res = max(res,dp[i]);
    cout<<res<<endl;
    return 0; 
}

单调栈

定义：

单调栈实际上就是栈，只是利用了一些巧妙的逻辑，使得每次新元素入栈后，栈内的元素都保持有序（单调递增或单调递减）。

单调栈用途不太广泛，只处理一种典型的问题，叫做 Next Greater Element。

凡是看到下一个更大或者下一个更小这一类的题用单调栈就完事了

单调栈类型模板(下一个更大元素)

首先，讲解 Next Greater Number 的原始问题：给你一个数组，返回一个等长的数组，对应索引存储着下一个更大元素，如果没有更大的元素，就存 -1。不好用语言解释清楚，直接上一个例子：

给你一个数组 [2,1,2,4,3]，你返回数组 [4,2,4,-1,-1]。

解释：第一个 2 后面比 2 大的数是 4; 1 后面比 1 大的数是 2；第二个 2 后面比 2 大的数是 4; 4 后面没有比 4 大的数，填 -1；3 后面没有比 3 大的数，填 -1。

这道题的暴力解法很好想到，就是对每个元素后面都进行扫描，找到第一个更大的元素就行了。但是暴力解法的时间复杂度是 O(n^2)。

这个问题可以这样抽象思考：把数组的元素想象成并列站立的人，元素大小想象成人的身高。这些人面对你站成一列，如何求元素「2」的 Next Greater Number 呢？很简单，如果能够看到元素「2」，那么他后面可见的第一个人就是「2」的 Next Greater Number，因为比「2」小的元素身高不够，都被「2」挡住了，第一个露出来的就是答案。

演示图片

#include <iostream>
#include <algorithm>
#include <cstring>
#include <stack>
using namespace std;
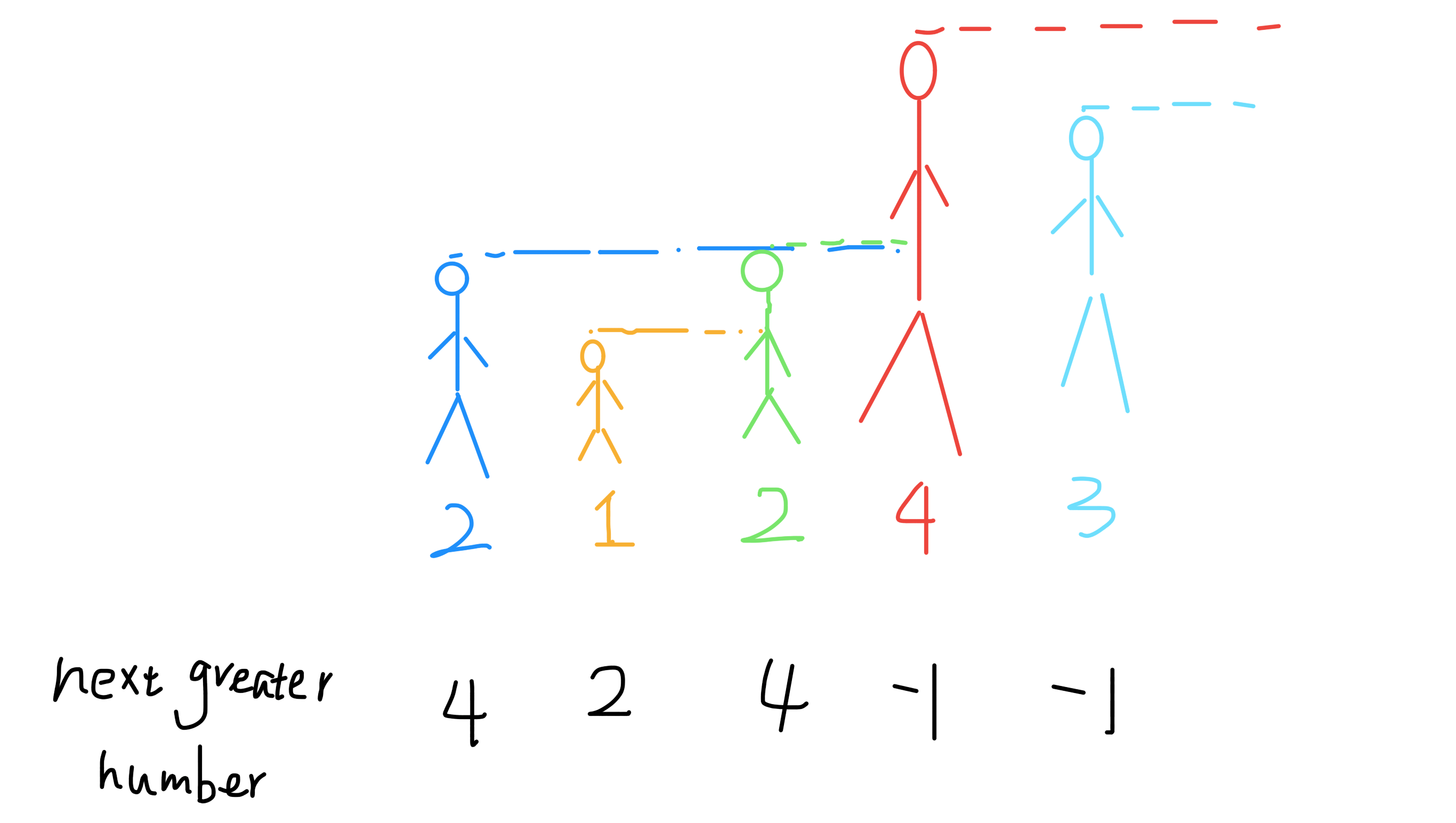
const int N=1e5+10;
int n;
int num[N],ans[N];
int main(){
    cin>>n;
    for(int i = 0;i<n;i++) cin>>num[i];
    stack<int> st;
    for(int i = n - 1;i>=0;i--){
        while(st.size() && st.top() <= num[i]){
            st.pop();
        }
        ans[i] = st.size()?st.top():-1;
        st.push(num[i]);
    }
    for(int i = 0;i<n;i++) cout<<ans[i]<<" ";
    return 0;
}

动态规划子问题 ----- 分苹果

样例题目

把M个弹珠放到N个盘子里面（我们允许有的盘子为空），你能求出有多少种分法吗？（请注意，例如有三个盘子，我们将5,1,1和1,1,5，视为同一种分法）

输入格式:
输入包含多组测试样例。每组输入的第一行是一个整数t。 接下来t行，每行输入两个整数M和N，代表有M个弹珠和N个盘子。（0=<M<=20; 0<N<=20）

输出格式:
对于每对输入的M和N，输出有多少种方法。

输入样例:
1
7 3
输出样例:
8

分析

1. 当我们的盘子数\(j\)多于弹珠数\(i\)时，即使我们每个盘子都放一个，也会有空出来的盘子，那么我们就可以将问题转换为\(i\)个盘子数\(i\)个弹珠有几种分法。
2. 当我们的盘子书\(j\)小于或等于\(i\)时，我们可以有两种选择：一种是现在每个盘子里至少放1个弹珠，那么问题可以转换为\(i-j\)个弹珠以及\(j\)个盘子有几种分法；另一种是我们允许空出来一个盘子（或者继续更多），那么问题就可以转换为在剩下\(j-1\)个盘子以及\(i\)个弹珠里有几种分法

\[ dp[i][j] = \begin{cases}dp[i][i] & \ j>i \\ dp[i-j][j] + dp[i][j-1] & j<=i\end{cases} \]

代码

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N=210,K = 10;
int dp[N][N];
int n,k;
int main()
{
    cin>>n>>k;
    for(int i = 0;i<=n;i++)	dp[i][0] = dp[0][i] = 1
    for(int i = 1;i<=n;i++){
        for(int j = 1;j<=k;j++){
            if(j>i)	dp[i][j] = dp[i][i];
            else dp[i][j] = dp[i-j][j] + dp[i][j-1];
        }
    }
    cout<<dp[n][k]<<endl;
    return 0;
}

洛谷P1025

题目描述

将整数 \(n\) 分成 \(k\) 份，且每份不能为空，任意两个方案不相同（不考虑顺序）。

例如：\(n=7\)，\(k=3\)，下面三种分法被认为是相同的。

\(1,1,5\);
\(1,5,1\);
\(5,1,1\).

问有多少种不同的分法。

输入格式

\(n,k\) （\(6<n \le 200\)，\(2 \le k \le 6\)）

输出格式

\(1\) 个整数，即不同的分法。

思路

思路类似于分苹果

1. 当分割数\(j\)大于数\(i\)的时候,那么没有一种分法可行
2. 当分割数\(j\)等于数\(i\)的时候,那么只有一种分法
3. 当分割数\(j\)小于数\(i\)的时候,一种是可以先在每个盘子里面分一个，问题可转换为分割术\(j\)分割 数\(i-j\)；另一种是可以将盘子数减少一个(或者更多)

代码

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N=210,K = 10;
int dp[N][N];
int n,k;
int main()
{
    cin>>n>>k;
    for(int i = 0;i<=n;i++) dp[i][i] = 1;
    for(int i = 1;i<=n;i++){
        for(int j = 1;j<=k;j++){
            dp[i][j] = dp[i-1][j-1] + dp[i - j][j];
        }
    }
    cout<<dp[n][k]<<endl;
    return 0;
}

状态压缩DP

基本思路

状态压缩DP其实是一种暴力的算法，因为它需要遍历每个状态，而每个状态是多个事件的集合，也就是以集合为状态，一个集合就是一个状态。集合问题一般是指数复杂度的NP问题，所以状态压缩DP的复杂度仍然是指数的，只能用于小规模问题的求解。

为了方便地同时表示一个状态的多个事件，状态一般用二进制数来表示。一个数就能表示一个状态，通常一个状态数据就是一个一串0和1组成的二进制数，每一位二进制数只有两种状态，比如说硬币的正反两面，10枚硬币的结果就可以用10位二进制数完全表示出来，每一个10位二进制数就表示了其中一种结果。

img

使用二进制数表示状态不仅缩小了数据存储空间，还能利用二进制数的位运算很方便地进行状态转移。

acwing291. 蒙德里安的梦想

求把 \(N \times M\) 的棋盘分割成若干个 1×21×2 的长方形，有多少种方案。

例如当 N=2，M=4时，共有 55 种方案。当 N=2，M=3 时，共有 33 种方案。

如下图所示：

2411_1.jpg

输入格式

输入包含多组测试用例。

每组测试用例占一行，包含两个整数 N 和 M。

当输入用例 N=0，M=0时，表示输入终止，且该用例无需处理。

输出格式

每个测试用例输出一个结果，每个结果占一行。

数据范围

1≤N,M≤11

输入样例：

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

输出样例：

1
0
1
2
3
5
144
51205

代码解释

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N=12,M=1<<N;
bool col_state[N];
long long dp[N][M];
vector<vector<int>> row_state(M);
int main()
{
    int n,m;
    while(cin>>n>>m){
        if(n == 0 && m == 0) break; 
        //两个都为0代表输入结束
        for(int i = 0;i<(1<<n);i++){ 
            //首先要预处理一列中的每一种状态，如果出现奇数个空格，那么就不能填满
            int cnt = 0; 
            //先初始化为0
            for(int j = 0;j<n;j++){ 
                //寻找每一位连续空闲的个数
                if((i>>j) & 1){ 
                    // 如果说当前被占用了，说明连续空闲已经结束
                    if(cnt & 1){
                        //判断连续空闲个数是否是奇数个，如果是的话，那么当前状态就有问题
                        col_state[i] = false;
                        break;
                    }
                    cnt = 0; 
                    // 当前连续空闲个数恢复成0
                }else{
                    cnt++; 
                    // 如果当前没被占用，那么连续空闲个数就加1
                }
            }
            if(cnt & 1) col_state[i] = false; 
            // 处理特殊情况，如果说当前二进制数最高位为0（没被占用的话）
           	// 那么我们就没办法判断末尾连续空闲个数是否为奇数，所以要特判
            else col_state[i] = true;
            //如果都是偶数，说明当前列中的状态是可行的。
        }
        
        for(int i = 0;i<(1<<n);i++){
            // 遍历第i列的每一种状态
            row_state[i].clear();
            // 清空当前预处理的值，否则可能会对下一输入的例子造成影响
            for(int j = 0;j<(1<<n);j++){
			// 遍历第i-1列的每一种状态
                if((j & i) == 0 && col_state[j | i]){
                    // 如果第i-1列在第i列要占用的对应格子是空出来的话，也就是格子占用了i-1列和i列，那么就没有冲突
                    // 同时因为第i-1列格子是由第i-2列延申出来的，同时第i列格子是从第i-1列延申出来的
                    // 所以第i列在j | i的对应格子都要被占用
                    row_state[i].push_back(j);
                    // 如果可行的话就加入数组中
                }
            }
        }
        
        memset(dp, 0, sizeof dp);  
        // 初始化
        dp[0][0] = 1; 
        // 因为第一列不能由-1列延申出来，所以第一列只有一种方法就是全部格子都不被占用
        for(int i = 1;i<=m;i++){ 
        // 遍历第2列到第m列，这里遍历到第m+1列是为了记录第m列没有凸出来的情况
            for(int j = 0;j<(1<<n);j++){
                // 遍历第i列每种可能的状态
                for(auto k:row_state[j]){ 
                    // 遍历在当前状态下，第i-1可行的方案
                    dp[i][j] += dp[i-1][k];
                }
            }
        }
        
        cout<<dp[m][0]<<endl; // 输出第m列且没有凸出来的情况
    }
    return 0;
}

离散化

离散化思想

为什么要离散化？

因为存储的下标实在太大了，如果直接开这么大的数组，根本不现实，第二个原因，本文是数轴，要是采用下标的话，可能存在负值，所以也不能，所以有人可能会提出用哈希表，哈希表可以吗？答案也是不可以的，因为哈希表不能像离散化那样缩小数组的空间，导致我们可能需要从-e9遍历到1e9（此处的含义就是假如我们需要计算1e-9和1e9区间内的值，那我们需要从前到后枚举，无论该值是否存在），因为哈希表不能排序，所以我们一般不能提前知道哪些数轴上的点存在哪些不存在，所以一般是从负的最小值到正的最大值都枚举一遍，时间负责度太高，于是就有了本题的离散化。

离散化的本质，是映射，将间隔很大的点，映射到相邻的数组元素中。减少对空间的需求，也减少计算量。

其实映射最大的难点是前后的映射关系，如何能够将不连续的点映射到连续的数组的下标。此处的解决办法就是开辟额外的数组存放原来的数组下标，或者说下标标志，本文是原来上的数轴上的非连续点的横坐标。 此处的做法是是对原来的数轴下标进行排序，再去重，为什么要去重呢，因为本题提前考虑了前缀和的思想，其实很简单，就是我们需要求出的区间内的和的两端断点不一定有元素，提前加如需要求前缀和的两个端点，有利于我们进行二分搜索，其实二分搜索里面我们一般假定有解的，如果没解的话需要特判，所以提前加入了这些元素，从而导致可能出现重复元素。

例题--ACwing区间和

假定有一个无限长的数轴，数轴上每个坐标上的数都是 00。

现在，我们首先进行 n 次操作，每次操作将某一位置 x上的数加 c。

接下来，进行 m次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [l,r] 之间的所有数的和。

输入格式

第一行包含两个整数 n和 m。

接下来 n行，每行包含两个整数 x 和 c。

再接下来 m行，每行包含两个整数 l 和 r。

输出格式

共 m 行，每行输出一个询问中所求的区间内数字和。

数据范围

\(-10^{9} < x < 10^{9}\)

\(1\le n,m \le 10^{5}\)

\(-10^{9}\le l \le r \le 10^{9}\)

\(-10000 \le c \le 10000\)

输入样例：

3 3
1 2
3 6
7 5
1 3
4 6
7 8

输出样例：

8
0
5

代码解释

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N=300010;
typedef pair<int,int> PII;
int a[N],s[N];
vector<int> alls;
// 记录所有需要离散化的数值
vector<PII> add,query;
// add用来存储对应点加的数，query用来存储查询区间
int find(int x){ 
    // 找到离散化后的下标
    int left = 0,right = alls.size();
    while(left<right){
        // 找到第一个大于等于x的数
        int mid = (left + right ) >> 1;
        if(alls[mid] >= x) right = mid;
        else left = mid + 1;
    }
    return left + 1;
    // 返回下表从1开始，因为这样构建前缀和比较方便
}
int main(){
    int n,m;
    cin>>n>>m;
    for(int i = 0;i<n;i++){ 
        int x,c;
        cin>>x>>c;
        add.push_back({x,c});
        alls.push_back(x);
    }
    for(int i = 0;i<m;i++){
        int left,right;
        cin>>left>>right;
        query.push_back({left,right});
        alls.push_back(left);
        // 将查询区间的左端点和右端点加入待离散化数组里
        // 如果不离散化的区间点的话，有可能出现该区间找不到离散化后的对应下标
        alls.push_back(right);
    }
    
    sort(alls.begin(),alls.end()); 
    // 进行排序
    alls.erase(unique(alls.begin(),alls.end()),alls.end());
    // 去除重复的元素，防止一个点离散化到多个下标上
    
    for(auto item:add){
        int x = find(item.first);
        a[x] += item.second;
    }
    // 构建差分矩阵
    
    for(int i = 1;i<=alls.size();i++)
        s[i] = s[i -1] + a[i];     
   // 构建前缀和矩阵
    
    for(auto item:query){
        int left = find(item.first);
        int right = find(item.second);
        cout<<s[right] - s[left - 1]<<endl;
    }
    // 找到区间对应的离散化后结果，然后运用前缀和进行求解
    
    return 0;
}

验证栈序列

题目描述

给出两个序列 pushed 和 poped 两个序列，其取值从 1 到 \(n(n\le100000)\)。已知入栈序列是 pushed，如果出栈序列有可能是 poped，则输出 Yes，否则输出 No。为了防止骗分，每个测试点有多组数据，不超过 \(5\) 组。

输入格式

第一行一个整数 \(q\)，询问次数。

接下来 \(q\) 个询问，对于每个询问：

第一行一个整数 \(n\) 表示序列长度；

第二行 \(n\) 个整数表示入栈序列；

第三行 \(n\) 个整数表示出栈序列；

输出格式

对于每个询问输出答案。

样例 #1

样例输入 #1

2
5
1 2 3 4 5
5 4 3 2 1
4
1 2 3 4
2 4 1 3

样例输出 #1

Yes
No

代码

可以这样理解，a序列不断入栈，直到遇到和b序列当前的数相同。然后依次再不断出栈，直到栈顶和b序列当前数不同。当a序列遍历完如果栈不为空那么就不是一个合格的出栈顺序，如果为空就是合格的出栈顺序。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
using namespace std;
const int N=1e6+10;
stack<int> st;
int a[N],b[N],num;
int main(){
    int n;
    cin>>n;
    while(n--){
        cin>>num;
        int cnt = 0;
        for(int i = 0;i<num;i++) cin>>a[i];
        for(int i = 0;i<num;i++) cin>>b[i];
        for(int i = 0;i<num;i++){
            st.push(a[i]);
            while(st.size() && st.top() == b[cnt]){
                st.pop();
                cnt ++;
            }
        }
        if(st.size()) cout<<"No"<<endl;
        else cout<<"Yes"<<endl;
        while(st.size()) st.pop();
    }
    return 0;
}

二分类题型

个人理解

如果题目出现了“最大值最小”、“最小值最大”、“第一个大于等于该数的值”（有序）、“最后一个小于等于该数的值”（有序）的情况下就可以考虑使用二分

二分模板1：（求第一个大于等于该数的值、最大值最小问题）

while(left<right){
	int mid = (left + right) >> 1;
	if(check(mid)) right = mid;
	else left = mid + 1;
}
cout<<left<<endl;

二分模板2：（求最后一个小于等于该数的值、最小值最大问题）

while(left < right){
	int mid = (left + right + 1) >> 1;
	if(check(mid)) left = mid;
	else right = mid - 1;
}
cout<<right<<endl;

1. 跳石头

题目描述

一年一度的“跳石头”比赛又要开始了！

这项比赛将在一条笔直的河道中进行，河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间，有 \(N\) 块岩石（不含起点和终点的岩石）。在比赛过程中，选手们将从起点出发，每一步跳向相邻的岩石，直至到达终点。

为了提高比赛难度，组委会计划移走一些岩石，使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制，组委会至多从起点和终点之间移走 \(M\) 块岩石（不能移走起点和终点的岩石）。

输入格式

第一行包含三个整数 \(L,N,M\)，分别表示起点到终点的距离，起点和终点之间的岩石数，以及组委会至多移走的岩石数。保证 \(L \geq 1\) 且 \(N \geq M \geq 0\)。

接下来 \(N\) 行，每行一个整数，第 \(i\) 行的整数 \(D_i\,( 0 < D_i < L)\)， 表示第 \(i\) 块岩石与起点的距离。这些岩石按与起点距离从小到大的顺序给出，且不会有两个岩石出现在同一个位置。

输出格式

一个整数，即最短跳跃距离的最大值。

样例

样例输入

25 5 2 
2
11
14
17 
21

样例输出

4

提示

输入输出样例说明

将与起点距离为 \(2\) 和 \(14\) 的两个岩石移走后，最短的跳跃距离为 \(4\)（从与起点距离 \(17\) 的岩石跳到距离 \(21\) 的岩石，或者从距离 \(21\) 的岩石跳到终点）。

数据规模与约定

对于 \(20\%\)的数据，\(0 \le M \le N \le 10\)。
对于 \(50\%\) 的数据，\(0 \le M \le N \le 100\)。
对于 \(100\%\) 的数据，\(0 \le M \le N \le 50000,1 \le L \le 10^9\)。

分析

如果直接去想做法会很困难，我们可以换一种思路去想。我们二分给定一个最小间隔距离，然后扫描一遍石头序列，如果不满足最小间隔就将该石头删去。

二分判断依据：如果删除的个数大于最多要求的个数，说明间隔大了，需要缩小范围 right=mid。如果删除个数小于等于最多个数，那么我们可以尝试继续变大间隔，left=mid+1；直到二分结束

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N=1e5+10;
int num[N];
int d,n,k;
int main(){
    cin>>d>>n>>k;
    int cur = 0;
    for(int i = 0;i<n;i++)  cin>>num[i];
    num[n] = d;
    int left = 0,right = 1e9;
    while(left<right){
        int mid = (left + right + 1) >> 1;
        int cnt = 0,cur = 0;
        for(int i = 0;i<=n;i++){
            if(num[i] - cur < mid) cnt++;
            else cur = num[i];
        }
        if(cnt <= k) left = mid;
        else right = mid - 1;
    }
    cout<<left<<endl;
    return 0;
}

2. 路标设置

题目背景

B 市和 T 市之间有一条长长的高速公路，这条公路的某些地方设有路标，但是大家都感觉路标设得太少了，相邻两个路标之间往往隔着相当长的一段距离。为了便于研究这个问题，我们把公路上相邻路标的最大距离定义为该公路的“空旷指数”。

题目描述

现在政府决定在公路上增设一些路标，使得公路的“空旷指数”最小。他们请求你设计一个程序计算能达到的最小值是多少。请注意，公路的起点和终点保证已设有路标，公路的长度为整数，并且原有路标和新设路标都必须距起点整数个单位距离。

输入格式

第 \(1\) 行包括三个数 \(L,N,K\)，分别表示公路的长度，原有路标的数量，以及最多可增设的路标数量。

第 \(2\) 行包括递增排列的 \(N\) 个整数，分别表示原有的 \(N\) 个路标的位置。路标的位置用距起点的距离表示，且一定位于区间 \([0,L]\) 内。

输出格式

输出 \(1\) 行，包含一个整数，表示增设路标后能达到的最小“空旷指数”值。

样例

样例输入

101 2 1
0 101

样例输出

51

提示

公路原来只在起点和终点处有两个路标，现在允许新增一个路标，应该把新路标设在距起点 \(50\) 或 \(51\) 个单位距离处，这样能达到最小的空旷指数 \(51\)。

\(50\%\) 的数据中，\(2 \leq N \leq 100\)，\(0 \leq K \leq 100\)。

\(100\%\) 的数据中，\(2 \leq N \leq 100000\), \(0 \leq K \leq100000\)。

\(100\%\) 的数据中，\(0 < L \leq 10000000\)。

分析

这道题思想和前面比较类似，我们可以用二分来寻找答案。我们设置一个间隔，当设置这个间隔所要插入的路标数大于最大插入数时，说明我们间隔小了，当小于等于最大插入数时，我们可以继续尝试缩小间隔。这题难点在于如何计算需要插入的数

代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
const int N=1e5+10;
int l,n,k;
int num[N];
// 这部分是难点
bool check(int mid){
    int cnt = k,cur = 0;
    for(int i = 1;i<n;i++){
        if(cnt < 0) break;
        if(num[i] - cur <= mid) cur = num[i];
        else{
            cur += mid;
            i --;
            cnt --;
        }
    }
    if(cnt < 0) return false;
    else return true;
}
// 
int main(){
    cin>>l>>n>>k;
    for(int i = 0;i<n;i++) cin>>num[i];
    int left = 0,right = l;
    int ans ;
    while(left<=right){
        int mid = left + (right - left) / 2 ;
        if(check(mid)){
            ans = mid;
            right = mid - 1;
        }
        else left = mid + 1;
    }
    cout<<ans<<endl;
    return 0;
}

分层最短路算法

定义

分层图最短路是指在可以进行分层图的图上解决最短路问题。分层图：可以理解为有多个平行的图。

一般模型是：在一个正常的图上可以进行 k 次决策，对于每次决策，不影响图的结构，只影响目前的状态或代价。一般将决策前的状态和决策后的状态之间连接一条权值为决策代价的边，表示付出该代价后就可以转换状态了。

一般有两种方法解决分层图最短路问题：

1. 建图时直接建成k+1层。
2. 多开一维记录机会信息。

第一种方法

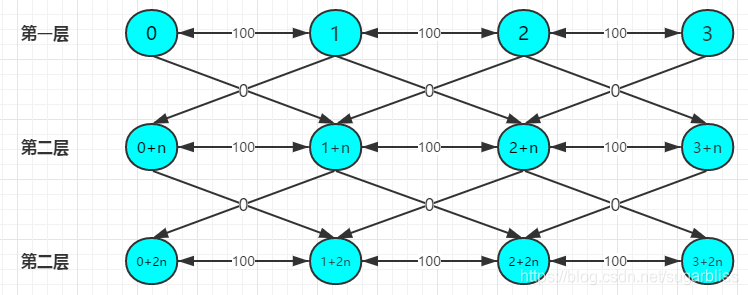
我们建\(k+1\)层图。然后有边的两个点，多建一条到下一层边权为0的单向边，如果走了这条边就表示用了一次机会。

有N个点时，\(1-n\)表示第一层，\((1+n)-(n+n)\)代表第三层\(,(1+2*n)-(n+2*n)\)代表第三层。因为要建K+1层图，数组要开到\(n*(k+1)\)，点的个数也为\(n*(k+1)\) 。

n = 4，m = 3， k = 2

0 1 100

1 2 100

2 3 100

建成图之后大概是这样的：

img

[JLOI2011] 飞行路线

题目描述

Alice 和 Bob 现在要乘飞机旅行，他们选择了一家相对便宜的航空公司。该航空公司一共在 \(n\) 个城市设有业务，设这些城市分别标记为 \(0\) 到 \(n-1\)，一共有 \(m\) 种航线，每种航线连接两个城市，并且航线有一定的价格。

Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市，途中可以进行转机。航空公司对他们这次旅行也推出优惠，他们可以免费在最多 \(k\) 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少？

输入格式

第一行三个整数 \(n,m,k\)，分别表示城市数，航线数和免费乘坐次数。

接下来一行两个整数 \(s,t\)，分别表示他们出行的起点城市编号和终点城市编号。

接下来 \(m\) 行，每行三个整数 \(a,b,c\)，表示存在一种航线，能从城市 \(a\) 到达城市 \(b\)，或从城市 \(b\) 到达城市 \(a\)，价格为 \(c\)。

输出格式

输出一行一个整数，为最少花费。

样例 #1

样例输入 #1

5 6 1
0 4
0 1 5
1 2 5
2 3 5
3 4 5
2 3 3
0 2 100

样例输出 #1

8

数据规模与约定

对于 \(30\%\) 的数据，\(2 \le n \le 50\)，\(1 \le m \le 300\)，\(k=0\)。

对于 \(50\%\) 的数据，\(2 \le n \le 600\)，\(1 \le m \le 6\times10^3\)，\(0 \le k \le 1\)。

对于 \(100\%\) 的数据，\(2 \le n \le 10^4\)，\(1 \le m \le 5\times 10^4\)，\(0 \le k \le 10\)，\(0\le s,t,a,b < n\)，\(a\ne b\)，\(0\le c\le 10^3\)。

另外存在一组 hack 数据。

方法

运用分层最短路算法，同层之间保持正常的距离图，从上层到下一层之间的距离为0（下层不能到上层），上层到下层代表着使用一次免费中转的机会。有k次免费中转的机会，所以要设置k+1层距离图。

代码

代码中最后求答案的时候要注意，我们在计算最小值的时候有可能没有把所有每次免费中转的机会都用完，所以要遍历每层中的终点值的解。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N=5e4*42;
int head[N],val[N],ne[N],w[N],dis[N],idx;
bool state[N];
int n,m,k,s,t;
void add(int a,int b,int c){
    ne[idx] = head[a];
    val[idx] = b;
    w[idx] = c;
    head[a] = idx++;
    return ;
}
int main(){
    cin>>n>>m>>k>>s>>t;
    memset(head,-1,sizeof head);
    memset(dis,0x3f,sizeof dis);
    while(m--){
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
        add(b,a,c);
        for(int i = 0;i<k;i++){
            add(a+i*n,b+(i+1)*n,0);
            add(b+i*n,a+(i+1)*n,0);
            add(a+(i+1)*n,b+(i+1)*n,c);
            add(b+(i+1)*n,a+(i+1)*n,c);
        }
    }
    dis[s] = 0;
    priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> q;
    q.push({0,s});
    while(q.size()){
        auto t = q.top();
        q.pop();
        if(state[t.second]) continue;
        int d = t.first;
        int node = t.second;
        state[node] = true;
        for(int i = head[node];i!=-1;i=ne[i]){
            int j = val[i];
            if(d + w[i] < dis[j] && !state[j]){
                dis[j] = d + w[i];
                q.push({dis[j],j});
            }
        }
    }
    int ans = dis[t];
    for(int i = 1;i<=k;i++) ans = min(ans,dis[t + k * n]);
    cout<<ans<<endl;
    return 0;
}

Leetcode 除自身以外数组的乘积

题目描述

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请 不要使用除法，且在 O(*n*) 时间复杂度内完成此题。

## 输入输出

示例 1:

输入: nums = [1,2,3,4]
输出: [24,12,8,6]

示例 2:

输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]

提示

• 2 <= nums.length <= 105
• -30 <= nums[i] <= 30
• 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内

解题思路

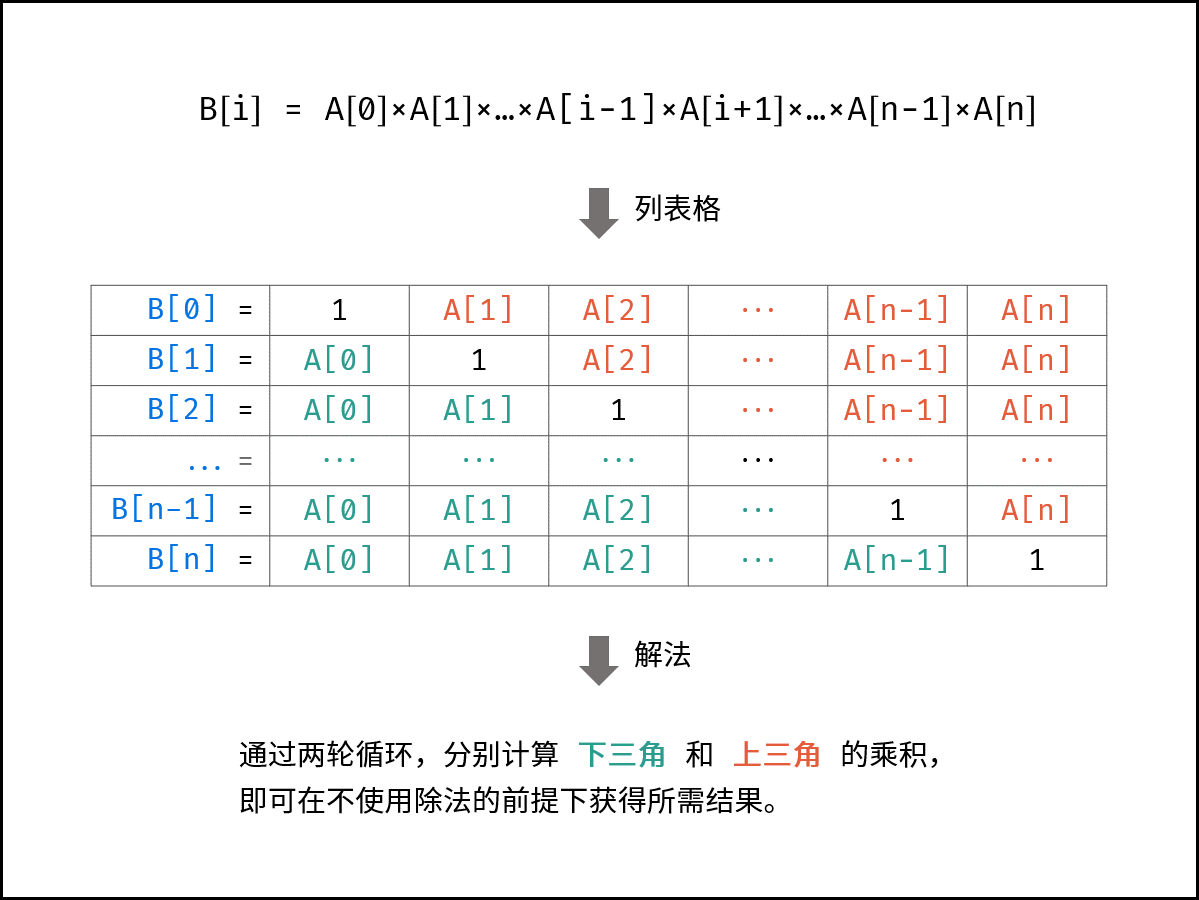
解题思路

代码编写

最朴素做法

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=1e5+10;
int nums[N],n;
int main(){
    cin>>n;
    for(int i = 0;i<n;i++) cin>>nums[i];
    int a[N],b[N],c[N];
    b[0] = 1;
    a[n-1] = 1;
    for(int i = 1;i<n;i++) b[i] = b[i-1] * nums[i-1];
    for(int i = n-2;i>=0;i--) a[i] = a[i+1] * nums[i+1];
    for(int i = 0;i<n;i++) c[i] = a[i] * b[i];
    for(int i = 0;i<n;i++) cout<<c[i]<<" ";
    cout<<endl;
    return 0; 
}

优化做法

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=1e5+10;
int nums[N],n;
int main(){
    cin>>n;
    for(int i = 0;i<n;i++) cin>>nums[i];
    int b[N],temp = 1;
    b[0] = 1;
    for(int i = 1;i<n;i++) b[i] = b[i-1] * nums[i-1];
    for(int i = n - 1;i>=0;i--){
        b[i] = b[i] * temp;
        temp = temp * nums[i];
    }
    for(int i = 0;i<n;i++) cout<<b[i]<<" ";
    cout<<endl;
    return 0; 
}

线性筛

筛素数

给定一个正整数 n𝑛，请你求出 1∼n1∼𝑛 中质数的个数。

输入格式

共一行，包含整数 n𝑛。

输出格式

共一行，包含一个整数，表示 1∼n1∼𝑛 中质数的个数。

数据范围

1≤n≤1061≤𝑛≤106

输入样例：

8

输出样例：

4

代码

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N=1e6+10;
int prime[N],n,cnt;
bool state[N];
int main(){
    cin>>n;
    for(int i = 2;i<=n;i++){
        if(!state[i]){
            prime[cnt++] = i;
        }
        for(int j = 0;prime[j] <= n / i ;j++){
            state[prime[j] * i] = true;
            if(i % prime[j] == 0) break;
        }
    }
    cout<<cnt<<endl;
    return 0;
}

理解

线性筛保证每次合数只被筛一次，通过将合数分解成\(x=prime[j]*i\),其中\(prime[j]\)是\(x\)的最小质因子。

如何保证\(prime[j]\)是\(x\)的最小质因子？

当\(i\space\ \% \space\ prime[j]\space\ != 0\)说明\(prime[j]\)比\(i\)的最小质因子还要小，当\(i\space\ \% \space\ prime[j]\space\ == 0\)的时候，\(prime[j]\)是\(i\)的质因子，因为我们是从小到达遍历质数，所以当\(i\space\ \% \space\ prime[j]\space\ == 0\)时停止遍历，就能保证\(x=prime[j]*i\)中\(prime[j]\)是\(x\)的最小质因子，否则我们不能保证\(prime[j]\)是\(i\)和\(x\)的最小质因数。

扩展欧几里得算法

acwing877 扩展欧几里得算法

给定\(n\)对正整数\(a_{i} b_{i}\)，对于每对数，求出一组\(x_{i} y_{i}\)，使其满足\(a_{i} x_{i} + b_{i} y_{i} = gcd(a_{i},b_{i})\)

输入格式

第一行包含整数 \(n\)。

接下来 \(n\) 行，每行包含两个整数\(a_{i} b_{i}\)

输出格式

输出共\(n\)行，对于每组\(a_{i} b_{i}\)，求出一组满足条件的\(x_{i} y_{i}\)，每组结果占一行。

本题答案不唯一，输出任意满足条件的\(x_{i} y_{i}\)均可。

数据范围

\(1\le n\le 10^{5}\) \(1 \le a_{i} ,b_{i} \le 2 \times 10^{9}\)

输入样例：

2
4 6
8 18

输出样例：

-1 1
-2 1

代码解决方法

// ax1 + by1 = gcd(a, b) = gcd(b,a % b)
// bx2 + (a - a / b * b)y2 = ax1 + by1
// bx2 + ay2 - a / b * y2 = ay2 + b(x2 - a / b * y2)

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
void exgcd(int a, int b, int &x, int &y){
    if(b == 0){
        x = 1, y = 0;
        return ;
    }else{
        exgcd(b, a % b, x, y);
        int t = x;
        x = y;
        y = t - a / b * y;
    }
}
int main(){
    int n;
    cin>>n;
    while(n--){
        int a,b,x,y;
        cin>>a>>b;
        exgcd(a,b,x,y);
        cout<<x<<" "<<y<<endl;
    }
    return 0;
}

acwing878 线性同余方程

给定n组数据\(a_{i} \space b_{i} \space m_{i}\)，对于每组数求出一个\(x_{i}\)，使其满足 \(a_{i} \space x_{i} \equiv b(mod \space \space m_{i})\)，如果无解则输出 impossible。

输入格式

第一行包含整数 n。

接下来 n 行，每行包含一组数据 \(a_{i} \space b_{i} \space m_{i}\)。

输出格式

输出共 n𝑛行，每组数据输出一个整数表示一个满足条件的\(x_{i}\)，如果无解则输出 impossible。

每组数据结果占一行，结果可能不唯一，输出任意一个满足条件的结果均可。

输出答案必须在 int范围之内。

数据范围

\(1\le n \le 10^{5}\) \(1 \le a_{i},b_{i},m_{i} \le 2 \times 10^{9}\)

输入样例：

2
2 3 6
4 3 5

输出样例：

impossible
-3

代码解决方案

因为\(ax \equiv b(mod \space \space m)\)等价于\(ax - b\)是\(m\)的倍数，因此线性同余方程问题可以转化为\(ax + my = b\)

根据裴蜀定理

裴蜀定理（或贝祖定理）得名于法国数学家艾蒂安·裴蜀，说明了对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性不定方程（称为裴蜀等式）：若a,b是整数,且gcd(a,b)=d，那么对于任意的整数x,y,ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立。

它的一个重要推论是：a,b互质的充分必要条件是存在整数x,y使ax+by=1.

所以上述方案有解的充分必要条件是\(gcd(a,m) | b\)

所以先对\(ax + my = b\)使用扩展欧几里得算法得到x，然后再对x进行放缩(\(b / gcd(a,m)\))即可得到答案

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
int exgcd(int a, int b,int &x,int &y){
    if(b == 0){
        x = 1,y = 0;
        return a;
    }
    int d = exgcd(b,a % b, x,y);
    int t = x;
    x = y;
    y = t - a / b * y;
    return d;
}

int main(){
    int n;
    cin>>n;
    while(n--){
        int a,b,m,x,y;
        cin>>a>>b>>m;
        int d = exgcd(a,m,x,y);
        if(b % d) cout<<"impossible"<<endl;
        else cout<<(ll)x * b / d % m<<endl;
    }
    return 0;
}