算法学习

排序

sort函数（sort和cmp配合使用）

sort函数（c++）可以对数据进行排序和自定义排序（cmp配合使用）

1
2
3
4
5
从小到大排序可以写成
sort(a,a+n,less<要进行排序的数据类型>())//a是数组的首地址，a+n是数组的尾地址(也可以是结构体数组)
从大到小排序可以写成
sort(a,a+n,greater<要进行排序的数据类型>())

sort可以和cmp函数配合使用进行自定义的结构体排序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
typedef struct //定义结构体
{
    char name[100];
    double a,b,c;
    double sum;
}student;
bool cmp(const student &a,const student &b)//cmp函数原型，其中形参要取地址，因为要变换原数据的位置
{
    if(a.sum!=b.sum) return a.sum>b.sum;
    else if(a.a!=b.a) return a.a>b.a;
    else if(a.b!=b.b) return a.b>b.b;
    else return a.c>b.c;
}
//cmp函数返回为true时不会变化位置，当返回false时会变换位置，所以return a.c>b.c就是降序排列，return a.c<b.c就是升序排序
int main()
{
    student a[10];
    sort(a,a+n,cmp);//进行自定义排序
}

堆排序

分析1：为什么从无序数组创建堆要从n/2开始？

因为堆为完全二叉树，完全二叉树中父亲和儿子的地址拥有如下关系：父亲X2=左儿子，父亲X2+1=右儿子，左儿子/2=右儿子/2=父亲。

分析2：升序和降序如何选择大根堆或者小根堆？

在升序中通常采用小根堆，在降序中采用大根堆。因为用数组模拟堆时，删除首元素比较麻烦，但是删除最后一个元素非常方便，直接让首元素等于最后一个元素，然后在不断down首元素得到正确的堆

分析3：为什么在down()函数中要不断递归呢？

因为创建堆的时候，当父亲比两个儿子都大的时候，我们找到三个中最小的一个，并交换位置，但是我们并不知道父亲在整个堆的位置，所以我们要不断down来正确找到父亲的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
//这里填你的代码^^
#include <iostream>
#include <string>
#include <queue>
using namespace std;
const int N=1e5+10;
int h[N],tt;
void down(int x)
{
    int t=x;
    if(2*x<=tt&&h[2*x]<h[t]) t=2*x;
    if(2*x+1<=tt&&h[2*x+1]<h[t]) t=2*x+1;//算出自己和自己的儿子谁小
    if(t!=x)//如果自己的儿子比自己小，就交换数值，并且递归让自己到达正确的位置
    {
        swap(h[x],h[t]);
        down(t);
    }
}
int main()
{
    int n,m;
    cin>>n>>m;
    ios::sync_with_stdio(false);
    tt=n;
    for(int i=1;i<=n;i++) cin>>h[i];//输入是无序的
    for(int i=n/2;i>0;i--) down(i);//为啥创建堆时权重是从n/2开始，因为最后一层不用进行堆的排序
    //要从最后一层的上一层开始，而父亲和儿子的权重关系是i(父亲)=i(儿子)*2
    for(int i=1;i<=m;i++)
    {
        cout<<h[1]<<" ";//最小的数，就是堆权重最小的数
        h[1]=h[tt--];//因为数组删除第一个元素时很困难的，所以直接将堆最后一位赋值到第一位
        down(1);//然后再判断该数是否在正确的位置
    }
    return 0;
}
//注意代码要放在两组三个点之间，才可以正确显示代码高亮哦~

桶排序

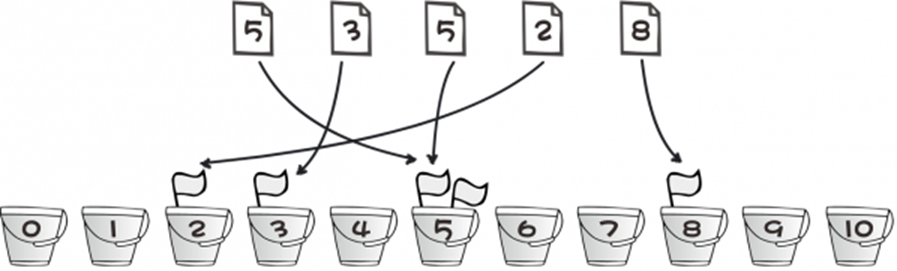
桶排序可以解决数据过多导致超时的情况，也可以计算计算得票数量类的题型

整个过程：

image-20220123164040471

例题：

1
2
3
4
5
6
为了找出林大2020新生中最擅长编写代码的同学，学校发起了一场投票。通过同学报名、前期遴选等环节，共提名了100名同学作为选举人进行评选，假设他们的编号从1到100。现在学院已经采集到了n名同学的投票结果，请你找出得票最多的程序员获得的票数(注：就是让你找相同数字的个数的最大值)。
输入样例1：
6
1 2 4 7 7 7
4
5 5 5 5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <bits/stdc++.h>
#include <algorithm>
using namespace std;
int a[200];
int main()
{
    int n,t;
    while(cin>>n)
    {
        memset(a,0,sizeof(a));//将数组初始化为0
        for(int i=1;i<=n;i++){//进行桶排序
            cin>>t;
            a[t]++;
        }
        int ans=0;
        for(int i=1;i<=100;i++) ans=max(ans,a[i]);//运用了max函数，max(a,b)函数会返回大的数
        cout<<ans<<endl;
    }
    return 0;
}

快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
785.快速排序

给定你一个长度为 n 的整数数列。

请你使用快速排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式
输入共两行，第一行包含整数 n。

第二行包含 n 个整数（所有整数均在 1∼109 范围内），表示整个数列。

输出格式
输出共一行，包含 n 个整数，表示排好序的数列。

数据范围
1≤n≤100000
输入样例：
5
3 1 2 4 5
输出样例：
1 2 3 4 5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N];

//模板
void quick_sort(int a[],int l,int r)
{
    if(l>=r) return;//递归结束条件
    int i=l-1,j=r+1,x=a[l+r>>1];//为什么要-1,因为在循环的时候会先加一
    while(i<j)
    {
        do i++;while(a[i]<x);//找到大于中间值的量
        do j--;while(a[j]>x);//找到小于中间值的量
        if(i<j) swap(a[i],a[j]);//如果i<j,就交换两个值
    }
    quick_sort(a,l,j);//进行二分递归
    quick_sort(a,j+1,r);
}


int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    quick_sort(a,0,n-1);
    for(int i=0;i<n;i++) i==n-1?cout<<a[i]<<endl:cout<<a[i]<<" ";
    return 0;
}

归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
787.归并排序

给定你一个长度为 n 的整数数列。

请你使用归并排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式
输入共两行，第一行包含整数 n。

第二行包含 n 个整数（所有整数均在 1∼109 范围内），表示整个数列。

输出格式
输出共一行，包含 n 个整数，表示排好序的数列。

数据范围
1≤n≤100000
输入样例：
5
3 1 2 4 5
输出样例：
1 2 3 4 5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
using namespace std;
const int N=1e6+10;
int q[N],tmp[N];
void merge_sort(int l,int r)
{
    if(l>=r) return;//递归结束条件
    int mid=l+r>>1;
    merge_sort(l,mid),merge_sort(mid+1,r);//递归二分到最小单元
    int k=0,i=l,j=mid+1;//两个数组部分的第一个元素
    while(i<=mid&&j<=r)//没有超过两个数组部分的最后一个位置
    {
        //有序合并两个数组
        if(q[i]<q[j]) tmp[k++]=q[i++];
        else tmp[k++]=q[j++];
    }
    while(i<=mid) tmp[k++]=q[i++];//如果还有剩余部分没有合并，就直接接上去
    while(j<=r) tmp[k++]=q[j++];
    for(k=0,i=l;i<=r;i++,k++) q[i]=tmp[k];//将有序的数组还原回原数组的对应位置，注意时对应位置
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++) cin>>q[i];
    merge_sort(0,n-1);
    for(int i=0;i<n;i++) i==n-1?cout<<q[i]<<endl:cout<<q[i]<<" ";
    return 0;
}

选择排序O(N^2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
787.归并排序

给定你一个长度为 n 的整数数列。

请你使用归并排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式
输入共两行，第一行包含整数 n。

第二行包含 n 个整数（所有整数均在 1∼109 范围内），表示整个数列。

输出格式
输出共一行，包含 n 个整数，表示排好序的数列。

数据范围
1≤n≤100000
输入样例：
5
3 1 2 4 5
输出样例：
1 2 3 4 5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
using namespace std;
const int N=1e6;
int a[N];
int main()
{
   int n;
   cin>>n;
   for(int i=0;i<n;i++) cin>>a[i];
   for(int i=0;i<n-1;i++)
   {
     for(int j=i+1;j<n;j++)
     {
       if(a[i]>a[j]) swap(a[i],a[j]); 
     }
   }
   for(int i=0;i<n;i++) cout<<a[i]<<"　";
   return 0;
}

冒泡排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
#define MAXSIZE 1000;
int a[1000];
void bubble_sort(int n)
{
    for(int i=0;i<=n;i++)
    {
        bool flag=true;
        for(int j=0;j<n-i;j++){
            if(a[j]>a[j+1]){
                swap(a[j],a[j+1]);
                flag=false;
            }
        }
        if(flag) break;
    }
}
int main()
{
    int n=0;
    int data;
    while(scanf("%d",&data)!=EOF)
    {
        if(!data){
            n--;
            break;
        }
        else a[n++]=data;
    }
    bubble_sort(n);
    for(int i=0;i<=n;i++) cout<<a[i]<<" ";
    cout<<endl;
    return 0;
}

直接插入算法

算法核心

从第二个元素开始，一旦有元素a[j-1]>a[j],那么就需要调整顺序。

先将a[j]存储到a[0],然后将a[j]=a[j-1],接着从j-2后往前比对，如果a[j]>a[0],那么就将a[j+1]=a[j],如果a[j]<=a[0],那么a[j+1]=a[0],结束本轮循环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
//直接插入排序算法
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
#define MAXSIZE 1000;
int a[1000];
void DirectInsertSort(int n)
{
    int j;
    for(int i=2;i<=n;i++)
    {
        if(a[i]<a[i-1])
        {
            a[0]=a[i];
            a[i]=a[i-1];
            for(j=i-2;a[0]<a[j];j--) a[j+1]=a[j];
            a[j+1]=a[0];
        }
    }
}
int main()
{
    int n=1;
    int data;
    while(scanf("%d",&data)!=EOF)
    {
        if(!data){
            n--;
            break;
        }
        else a[n++]=data;
    }
    DirectInsertSort(n);
    for(int i=1;i<=n;i++) cout<<a[i]<<" ";
    cout<<endl;
    return 0;
}

二进制枚举

详细介绍二进制枚举

1.含有N个元素的集合的一切子集个数有2^n种，二进制采用0和1来表示数字。于是我们可以利用二进制特性，将含n个元素都用0和1来表示选和不选，于是就可以得到每一种子集的情况。

2.那我们如何找到每个位置是否选和不选？可以采用位运算和与运算结合的方式。<<运算相当于在01串的尾巴处加上0（左移一位相当于乘以2），而与运算的规则是全为1才可以得到1。那么我们就可以通过对1不断进行左移运算和与运算得到每个位置的选择情况

1
2
3
4
5
6
7
1<<1=2(10);  1000&0010=0000

1<<2=4(100); 1000&0100=0000

1<<3=8(1000); 1000&1000=1000

1<<4=16(10000); 01000&10000=00000

例题：

和为K--二进制枚举

1
2
3
4
5
6
7
8
9
10
11
12
Description
给出长度为n的数组,求能否从中选出若干个,使他们的和为K.如果可以,输出:Yes,否则输出No
Input
第一行：输入N,K,为数组的长度和需要判断的和(2<=N<=20,1<=K<=10^9)
第二行：N个值，表示数组中元素的值(1<=a[i]<=10^6)
Output
输出Yes或No
Sample Input
5 13
2 4 6 8 10
Sample Output
No
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n,k;
    while(cin>>n>>k)
    {
        int a[n];
        for(int i=0;i<n;i++) cin>>a[i];
        int flag=1;
        for(int i=0;i<(1<<n);i++)//共有1<<n种子集，遍历每种子集
        {
            int sum=0;
            for(int j=0;j<n;j++)//遍历每个位置
            {
                if(i&(1<<j))  sum+=a[j];//如果选择该位置，就加上该位置的值
            }
            if(sum==k){
                cout<<"Yes"<<endl;
                flag=0;
                break;
            }
        }
        if(flag) cout<<"No"<<endl;
     }
    return 0;
}

陈老师加油-二进制枚举

1
2
3
4
5
6
7
8
9
10
11
12
Description
陈老师经常开车在哈尔滨的大街上行走，假设刚开始油箱里有T升汽油，每看见加油站陈老师就要把汽油的总量翻倍（就是乘2）；每看见十字路口气油就要减少1升；最后的时候陈老师的车开到一个十字路口，然后车就没油了------就熄火了，陈老师好痛苦啊~~~！
然后他就开始回忆，一路上一共遇到5个加油站，10个十字路口，问造成这种惨烈的境遇有多少种可能？

Input
输入一个T ，（1<=T<=100）;
Output
输出可能的方案数。
Sample Input
1
Sample Output
10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
#include <algorithm>
using namespace std;
int main()
{
    int n;
    while(cin>>n)
    {
        int ans=0;
        for(int i=0;i<(1<<15);i++)//遍历每种情况
        {
            int a=0,b=0,tmp=n;
            for(int j=0;j<15;j++)
            {
              if(i&(1<<j)){//可以假设选取该位置为加油站
                  tmp*=2;
                  a++;
              }
              else{//不选取该位置为十字路口
                  tmp-=1;
                  b++;
              }
              if(tmp<=0) break;
            }
            if(tmp==0&&a==5&&b==10) ans++;//满足题目条件的情况就加上1
        }
        cout<<ans<<endl;
    }
    return 0;
}

权利指数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Description
在选举问题中，总共有n个小团体，每个小团体拥有一定数量的选票数。如果其中m个小团体的票数和超过总票数的一半，则此组合为“获胜联盟”。n个团体可形成若干个获胜联盟。一个小团体要成为一个“关键加入者”的条件是：在其所在的获胜联盟中，如果缺少了这个小团体的加入，则此联盟不能成为获胜联盟。一个小团体的权利指数是指：一个小团体在所有获胜联盟中成为“关键加入者”的次数。请你计算每个小团体的权利指数。
Input
输入数据的第一行为一个正整数T，表示有T组测试数据。每一组测试数据的第一行为一个正整数n（0<n<=20）。第二行有n个正整数，分别表示1到n号小团体的票数。
Output
对每组测试数据，在同一个行按顺序输出1到n号小团体的权利指数。
Sample Input
2
1
10
7
5 7 4 8 6 7 5
Sample Output
1
16 22 16 24 20 22 16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h>
#include <algorithm>
using namespace std;
int main()
{
    int k;
    cin>>k;
    while(k--)
    {
        int x,a[20],sum=0,flag[20],b[20],ans;//注意总数再每组数据时要清零，我就栽在这非常久
        cin>>x;
        memset(b,0,sizeof(b));//memset下保证上次数据不会影响
        for(int i=0;i<x;i++){
            cin>>a[i];
            sum+=a[i];
        }
        for(int i=0;i<(1<<x);i++)
        {
            memset(flag,0,sizeof(flag));//这里是关键，用flag记录每种子集选取了哪些位置，以便下面查找情况
            ans=0;
            for(int j=0;j<x;j++)
            {
                if(i&(1<<j))
                { ans+=a[j];flag[j]=1;}
            }
            if(ans<=sum/2){//满足题目条件，找本来不满足，多了一个位置后就可以满足的情况。
                for(int z=0;z<x;z++)
                {
                    if(flag[z]==0&&ans+a[z]>sum/2) b[z]++;
                }
            }
            /*if(ans>=sum/2){//我原本是顺着题目意思写的，但这里我还不清楚为啥这样写oj过不去
                for(int z=0;z<x;z++)
                {
                    if(flag[z]==1&&ans-a[z]<sum/2) b[z]++;
                }
            }*/
        }
        for(int i=0;i<x-1;i++) cout<<b[i]<<" ";
        cout<<b[x-1]<<endl;
    }
    return 0;
}

二分

整数二分

二分模板1:（求下标最小的x）

1
2
3
4
5
6
7
8
while(l<r)
{
   int mid=l+r>>1;
   if(a[mid]>=x) r=mid;
   else l=mid+1;
}
//l的范围时[l,mid],r的范围时(mid,r]
//当l+r>>1时是向下取整，所以不用担心死循环

二分模板2：（求下标最大的x）

1
2
3
4
5
6
7
8
while(l<r)
{
   int mid=l+r+1>>1;
   if(a[mid]<=x) l=mid;
   else r=mid-1;
}
//l的范围时[l,mid),r的范围时[mid,r]
//当mid=l+r+1>>1 因为在特殊条件下有可能死循环，当只有两个数，且正好按要求排序了的时候，如果选l+r>>1，因为会向下取整导致死循环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
789 数的范围

给定一个按照升序排列的长度为 n 的整数数组，以及 q 个查询。

对于每个查询，返回一个元素 k 的起始位置和终止位置（位置从 0 开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

输入格式
第一行包含整数 n 和 q，表示数组长度和询问个数。

第二行包含 n 个整数（均在 1∼10000 范围内），表示完整数组。

接下来 q 行，每行包含一个整数 k，表示一个询问元素。

输出格式
共 q 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回 -1 -1。

数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000
输入样例：
6 3
1 2 2 3 3 4
3
4
5
输出样例：
3 4
5 5
-1 -1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
using namespace std;
const int N=1e5+10;
int q[N],n,m;
int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++) scanf("%d",&q[i]);
    while(m--)
    {
        int k;
        cin>>k;
        int l=0,r=n-1;
        while(l<r){
            int mid=l+r>>1;
            if(q[mid]>=k) r=mid;//找最早出现的k，那么k后的数都满足大于等于k
            else l=mid+1;
        }
        if(q[l]!=k) cout<<"-1 -1"<<endl;
        else 
        {
            cout<<l<<" ";
            int l=0,r=n-1;
            while(l<r){
                int mid=l+r+1>>1;
                if(q[mid]<=k) l=mid;//找最后出现的k,那么k前面的数都满足小于等于k
                else r=mid-1;
            }
            cout<<l<<endl;
        }
    }
    return 0;
}

浮点数二分

模板

1
2
3
4
5
6
7
while(r-l>1e-6)
{
  mid=(l+r)/2;
  if(check(mid)) r=mid;
  else l=mid;
}
//当r-l<1e-8的时候，r和l的值可以近似认为是答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
给定一个浮点数 n，求它的三次方根。

输入格式
共一行，包含一个浮点数 n。

输出格式
共一行，包含一个浮点数，表示问题的解。

注意，结果保留 6 位小数。

数据范围
−10000≤n≤10000
输入样例：
1000.00
输出样例：
10.000000
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <iostream>
using namespace std;
int main()
{
    double x;
    cin>>x;
    double l=-10000,r=10000;
    while(r-l>1e-8)
    {
        double mid=(l+r)/2;
        if((mid*mid*mid)>=x) r=mid;
        else l=mid;
    }
    printf("%.6lf",l);
    return 0;
}

高精度

高精度加法

高精度加法关键在于将每一位数字拆解，然后逆向存入数组里（比如输入进来1234，在传入数组中的时候值为4321，然后再利用小学数学加法的知识，每一位数字的值为A[I]+B[I]+t(t为进位的值)，循环进行直到遍历到数组a和b的结束位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
给定两个正整数（不含前导 0），计算它们的和。

输入格式
共两行，每行包含一个整数。

输出格式
共一行，包含所求的和。

数据范围
1≤整数长度≤100000
输入样例：
12
23
输出样例：
35
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
#include <vector>
#include <string>
using namespace std;
vector<int> add(const vector<int>&A,const vector<int>&B)//为啥是传入指针，因为数组A和B的内存过大，如果传入形参会导致内存溢出
{
    vector<int> C;
    int t=0;//进位
    for(int i=0;i<A.size()||i<B.size();i++)//遍历到数组A或数组B结束位置
    {
        if(i<A.size()) t+=A[i];//如果没到A结束位置就加上该位置的值
        if(i<B.size()) t+=B[i];
        C.push_back(t%10);//传入未进位的部分，比如t=18,在算数中，1进位，然后7传入
        t/=10;//记录下进位的数
    }
    if(t) C.push_back(1);
    return C;
}
int main()
{
    string a,b;//因为数据过大，只能用字符串形式传入
    vector<int>A,B;
    cin>>a>>b;//a="1234"
    for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');//逆向计入每一位的值 A[]=[4,3,2,1]
    for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
    auto C=add(A,B);
    for(int i=C.size()-1;i>=0;i--) cout<<C[i];
    return 0;
}

leetcode66题

1
2
3
4
5
6
66. 加一
给定一个由 整数 组成的 非空 数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位， 数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/*我的做法,相对麻烦了点，和模板的高精度加法类似*/
class Solution {
public:
    vector<int> plusOne(vector<int>& digits) {
          vector<int> ans;
          int t=1;
          for(int i=digits.size()-1;i>=0;i--)
          {
              t+=digits[i];
              ans.push_back(t%10);
              t/=10;
          }
          if(t) ans.push_back(1);
          reverse(ans.begin(),ans.end());
          return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
/*题解的做法，就是找到从尾巴开始的最长的9，如果从尾部开始有9就变成0，然后往前移动，如果超出了最开头，就把vector加一*/
class Solution {
public:
    vector<int> plusOne(vector<int>& digits) {
        int i=digits.size()-1;
        while(i>=0&&digits[i]==9)
        {
           digits[i]=0;
           i--;
        }
        if(i==-1) digits.insert(digits.begin(),1);
        else digits[i]+;
        return digits;
};

leetcode第二题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
2. 两数相加
给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。
示例 1：
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.
示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]
示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]
 

提示：

每个链表中的节点数在范围 [1, 100] 内
0 <= Node.val <= 9
题目数据保证列表表示的数字不含前导零
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode* head=new ListNode(-1),*pMove=head;
        int t=0;
        while(l1||l2||t)
        {
           if(l1) t+=l1->val;
           if(l2) t+=l2->val;
           pMove->next=new ListNode(t%10);
           t/=10;
           pMove=pMove->next;
            /*这个很重要，因为如果用for语句的话，当l1没有时还想下找就会报错*/
           if(l1) l1=l1->next;
           if(l2) l2=l2->next;
        }
        return head->next;
    }
};

高精度减法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
给定两个正整数（不含前导 0），计算它们的差，计算结果可能为负数。

输入格式
共两行，每行包含一个整数。

输出格式
共一行，包含所求的差。

数据范围
1≤整数长度≤105
输入样例：
32
11
输出样例：
21
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <vector>
#include <string>
using namespace std;
bool cmp(vector<int>&A,vector<int>&B)
{
    if(A.size()!=B.size()) return A.size()>B.size();//如果长度不一样就判断A是否长于B
    else
       for(int i=A.size();i>=0;i--)//遍历知道找到第一个不一样的数，判断A[i]是否大于B[i]
        if(A[i]!=B[i]) return A[i]>B[i];
    return true;//如果循环到结束说明一样长，成真和成假都可以
}
vector<int> sub(const vector<int>&A,const vector<int>&B)
{
    vector<int>C;
    for(int i=0,t=0;i<A.size();i++)
    {
        t=A[i]-t;//算上是否有进位
        if(i<B.size()) t-=B[i];//如果在B的范围内就减去B[i]
        C.push_back((t+10)%10);//如果A[i]-t>B[i]的话,+10取余不会有任何影响，但是如果小于的话加10取余就相当于进位
        if(t<0) t=1;//判断石是否需要进位
        else t=0;
    }
    while(C.size()>1&&C.back()==0) C.pop_back();//消去前置零 比如003，要消去00，得出3，因为高位在后面，所以只需要判断back时候是零，如果是零的话，就pop出来
    return C;
}
int main()
{
    string a,b;
    vector<int> A,B;
    cin>>a>>b;
    for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');//别忘了传进来的是字符串，转化成数字需要减去'0'
    for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
    if(cmp(A,B))//进行比较是否A>B，如果大于的话就正常的进行相加减，如果小于的话就转换成B-A，然后加负号
    {
        auto C=sub(A,B);
        for(int i=C.size()-1;i>=0;i--) cout<<C[i];//传入的时候是个位数开始到最高位，所以输出的时候要倒着输出
    }
    else{
        auto C=sub(B,A);
        cout<<"-";
        for(int i=C.size()-1;i>=0;i--) cout<<C[i];
    }
    return 0;
}

##　高精度乘法

高精度X低精度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
#include <vector>

using namespace std;

vector <int> mul(vector <int> & A, int b) {
    vector <int> C;

    int t = 0;
    for (int i = 0; i < A.size(); i ++) {
        t += A[i] * b;       // t + A[i] * b = 7218
        C.push_back(t % 10); // 只取个位 8
        t /= 10;             // 721 看作 进位
    }

    while (t) {            // 处理最后剩余的 t
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}

int main() {
    string a;
    int b;
    cin >> a >> b;

    vector <int> A;
    for (int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - '0');

    auto C = mul(A, b);

    for (int i = C.size() - 1; i >= 0; i --) {
        cout << C[i];
    }

    return 0;
}

高精度X高精度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <vector>

using namespace std;

vector<int> mul(vector<int> &A, vector<int> &B) {
    vector<int> C(A.size() + B.size() + 7, 0); // 初始化为 0，C的size可以大一点

    for (int i = 0; i < A.size(); i++)
        for (int j = 0; j < B.size(); j++)
            C[i + j] += A[i] * B[j];

    int t = 0;
    for (int i = 0; i < C.size(); i++) { // i = C.size() - 1时 t 一定小于 10
        t += C[i];
        C[i] = t % 10;
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back(); // 必须要去前导 0，因为最高位很可能是 0
    return C;
}

int main() {
    string a, b;
    cin >> a >> b; // a = "1222323", b = "2323423423"

    vector<int> A, B;
    for (int i = a.size() - 1; i >= 0; i--)
        A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i--)
        B.push_back(b[i] - '0');

    auto C = mul(A, B);

    for (int i = C.size() - 1; i >= 0; i--)
        cout << C[i];

    return 0;
}

acwing例题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
793 高精度乘法

给定两个非负整数（不含前导 0） A 和 B，请你计算 A×B 的值。

输入格式
共两行，第一行包含整数 A，第二行包含整数 B。

输出格式
共一行，包含 A×B 的值。

数据范围
1≤A的长度≤100000,
0≤B≤10000
输入样例：
2
3
输出样例：
6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
高精度乘以低精度
#include <iostream>
#include <vector>
#include <string>
using namespace std;
vector<int> mul(vector<int>&A,int b)
{
    vector<int> C;
    int t=0;
    for(int i=0;i<A.size();i++)//讲每一位都乘以b，然后去进位
    {
        t+=A[i]*b;
        C.push_back(t%10);
        t/=10;
    }
    while(t)//如果还有进位没去完就一直取，取到结束为止
    {
        C.push_back(t%10);
        t/=10;
    }
    while(C.size()>1&&C.back()==0) C.pop_back(); //如果有前置零，要去掉前置零
    return C;
}
int main()//常规操作
{
    string a;
    int b;
    vector<int> A;
    cin>>a>>b;
    for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
    auto C=mul(A,b);
    for(int i=C.size()-1;i>=0;i--) cout<<C[i];
    return 0;
}

高精度除法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
给定两个非负整数（不含前导 0） A，B，请你计算 A/B 的商和余数。

输入格式
共两行，第一行包含整数 A，第二行包含整数 B。

输出格式
共两行，第一行输出所求的商，第二行输出所求余数。

数据范围
1≤A的长度≤100000,
1≤B≤10000,
B 一定不为 0
输入样例：
7
2
输出样例：
3
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
vector<int> divide(vector<int>&A,int b,int&r)//将余数传入，利用余数来求值
{
    vector<int> C;
    for(int i=A.size()-1;i>=0;i--)//除法就是上一位的余数*10+这一位然后再除以除数反复得到答案
    {
        r=r*10+A[i];
        C.push_back(r/b);
        r%=b;
    }
    reverse(C.begin(),C.end());//因为是正向存储，所以reverse一下
    while(C.size()>1&&C.back()==0) C.pop_back();//删除前置零
    return C;
}
int main()//前面都一样
{
    string a;
    int b,r=0;
    cin>>a>>b;
    vector<int> A;
    for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
    auto C=divide(A,b,r);
    for(int i=C.size()-1;i>=0;i--) cout<<C[i];
    cout<<endl<<r<<endl;
    return 0;
}

leetcode67题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
67. 二进制求和
给你两个二进制字符串，返回它们的和（用二进制表示）。
输入为 非空 字符串且只包含数字 1 和 0。

示例 1:
输入: a = "11", b = "1"
输出: "100"
示例 2:
输入: a = "1010", b = "1011"
输出: "10101"

提示：
每个字符串仅由字符 '0' 或 '1' 组成。
1 <= a.length, b.length <= 10^4
字符串如果不是 "0" ，就都不含前导零。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//高精度加法的思想
class Solution {
public:
    string addBinary(string a, string b) {
       vector<int>A,B;
       for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
       for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
       string C;
       int t=0;
       for(int i=0;i<A.size()||i<B.size();i++)
       {
           if(i<A.size()) t+=A[i];
           if(i<B.size()) t+=B[i];
           C+=(t%2+'0');
           t/=2;
       }
       if(t) C+=(1+'0');
       reverse(C.begin(),C.end());
       return C;
    }
};

前缀和

一维前缀和

将A[1]+......A[n] (n为变量)的值一一单独存入另一个数组中，然后查找区间的前缀和时，只要S[R]-S[L-1]即可得到区间前缀和（为啥是l-1，因为S[R]=A[1]+....A[R]，S[L-1]=A[1]+....+A[L-1],两个相减就可以得到A[L]+...+A[R]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
795 前缀和
输入一个长度为 n 的整数序列。

接下来再输入 m 个询问，每个询问输入一对 l,r。

对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。

输入格式
第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

接下来 m 行，每行包含两个整数 l 和 r，表示一个询问的区间范围。

输出格式
共 m 行，每行输出一个询问的结果。

数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例：
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例：
3
6
10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
using namespace std;
const int N = 1e5+10;
int q[N],s[N];
int main()
{
    ios::sync_with_stdio(false);
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>q[i];
    for(int i=1;i<=n;i++) s[i]=s[i-1]+q[i];
    while(m--)
    {
        int l,r;
        cin>>l>>r;
        cout<<s[r]-s[l-1]<<endl;
    }
    return 0;
}

leetcode303

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
303. 区域和检索 - 数组不可变
给定一个整数数组  nums，处理以下类型的多个查询:

计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的 和 ，其中 left <= right
实现 NumArray 类：

NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + ... + nums[right] )
 

示例 1：

输入：
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出：
[null, 1, -1, -3]

解释：
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) 
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))
 

提示：

1 <= nums.length <= 104
-105 <= nums[i] <= 105
0 <= i <= j < nums.length
最多调用 104 次 sumRange 方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class NumArray {
public:
    vector<int>sum;
    NumArray(vector<int>& nums) {
        sum.push_back(0);
        for(int i=1;i<=nums.size();i++)
           sum.push_back(sum[i-1]+nums[i-1]);
    }
    
    int sumRange(int left, int right) {
       return sum[right+1]-sum[left];
    }
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * int param_1 = obj->sumRange(left,right);
 */

二维前缀和

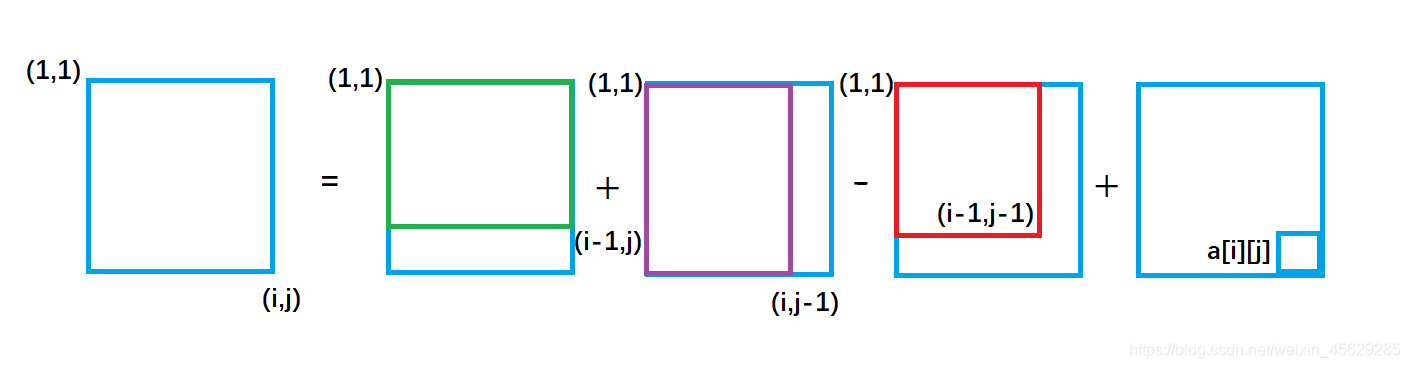
二维前缀和推导 如图：

紫色面积是指(1,1)左上角到(i,j-1)右下角的矩形面积, 绿色面积是指(1,1)左上角到(i-1, j )右下角的矩形面积。每一个颜色的矩形面积都代表了它所包围元素的和。在这里插入图片描述

从图中我们很容易看出，整个外围蓝色矩形面积s[i] [j] = 绿色面积s[i-1] [j] + 紫色面积s[i] [j-1] - 重复加的红色的面积s[i-1] [j-1]+小方块的面积a[i] [j];

因此得出二维前缀和预处理公式

s[i] [j] = s[i-1] [j] + s[i] [j-1 ] + a[i] [j] - s[i-1] [ j-1] (是离散的数，不是面积哈)

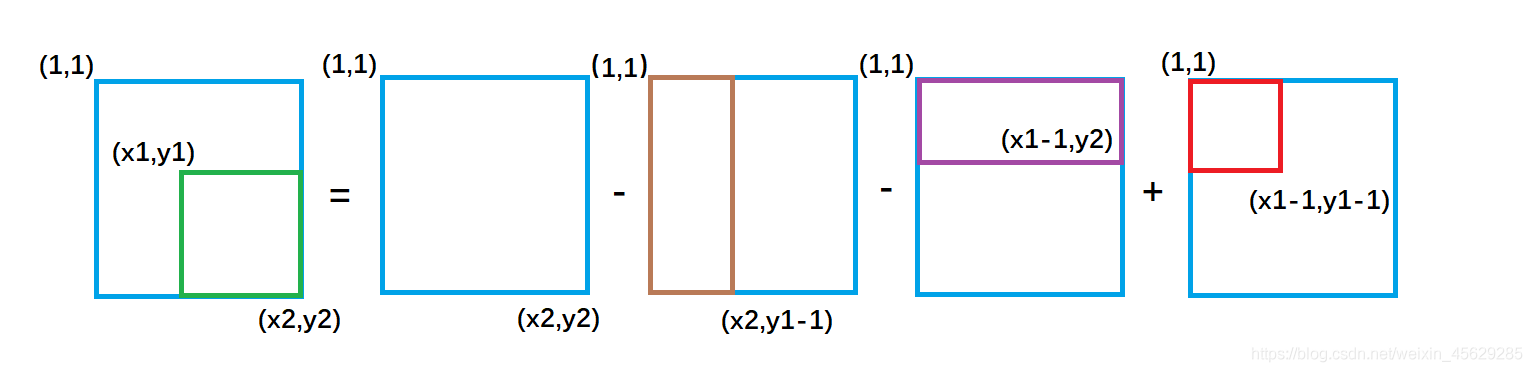
接下来回归问题去求以(x1,y1)为左上角和以(x2,y2)为右下角的矩阵的元素的和。

如图：

紫色面积是指 ( 1,1 )左上角到(x1-1,y2)右下角的矩形面积 ，黄色面积是指(1,1)左上角到(x2,y1-1)右下角的矩形面积；

不难推出：在这里插入图片描述

绿色矩形的面积 = 整个外围面积s[x2, y2] - 黄色面积s[x2, y1 - 1] - 紫色面积s[x1 - 1, y2] + 重复减去的红色面积 s[x1 - 1, y1 - 1]

因此二维前缀和的结论为：

以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为： s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
796 二维前缀和
输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数 n，m，q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。

输出格式
共 q 行，每行输出一个询问的结果。

数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例：
17
27
21
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<iostream>
using namespace std;
const int N=1e3+10;
int a[N][N],s[N][N];
int main()
{
    int n,m,q;
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
       scanf("%d",&a[i][j]);
    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
         s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
    while(q--)
    {
        int x1,x2,y1,y2;
        cin>>x1>>y1>>x2>>y2;
        printf("%d\n",s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]);
    }
    return 0;
}

leetcode304

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
304. 二维区域和检索 - 矩阵不可变
给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。
实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。
 

示例 1：
自己取leetcode上看吧
输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)
 

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-105 <= matrix[i][j] <= 105
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
最多调用 104 次 sumRegion 方法
通过次数86,115提交次数148,070
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class NumMatrix {
public:
    int sum[2000][2000];
    NumMatrix(vector<vector<int>>& matrix) {
       int n=matrix.size(),m=matrix[0].size();//获得vector数组的列数和每行长度
       if(n>0){
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+matrix[i-1][j-1];//最后matrix[i-1][j-1]是因为我们是从i=1,j=1开始，但是原数组是从i=0,j=0开始
       }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        return sum[row2+1][col2+1]-sum[row1][col2+1]-sum[row2+1][col1]+sum[row1][col1];
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * int param_1 = obj->sumRegion(row1,col1,row2,col2);
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class NumMatrix {
public:
    vector<vector<int>> sum;//vector数组
    NumMatrix(vector<vector<int>>& matrix) {
       int n=matrix.size(),m=matrix[0].size();//获得原数组的列数和每行长度
       if(n>0){
        sum.resize(n+1,vector<int>(m+1,0));//多加一行和一列，从第一行和第一列开始
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+matrix[i-1][j-1];//最后matrix[i-1][j-1]是因为我们是从i=1,j=1开始，但是原数组是从i=0,j=0开始
       }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        return sum[row2+1][col2+1]-sum[row1][col2+1]-sum[row2+1][col1]+sum[row1][col1];
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * int param_1 = obj->sumRegion(row1,col1,row2,col2);
 */

差分

一维差分

详细知识链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
输入一个长度为 n 的整数序列。

接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。

输出格式
共一行，包含 n 个整数，表示最终序列。

数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例：
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例：
3 4 5 3 4 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int main()
{
    ios::sync_with_stdio(false);
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) b[i]=a[i]-a[i-1];
    while(m--)
    {
        int l,r,c;
        cin>>l>>r>>c;
        b[l]+=c;
        b[r+1]-=c;
    }
    for(int i=1;i<=n;i++) a[i]=a[i-1]+b[i];
    for(int i=1;i<=n;i++) cout<<a[i]<<" ";
    return 0;
}

y总版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
void insert(int l,int r,int c)
{
    b[l]+=c;
    b[r+1]-=c;
}
int main()
{
    int n,m;
    cin>>n>>m;
    ios::sync_with_stdio(false);
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) insert(i,i,a[i]);//插入每一个数，并再下一个数后减去该数，在进行b[i]+=b[i-1]时就可以得到b[i]
    while(m--)
    {
        int l,r,c;
        cin>>l>>r>>c;
        insert(l,r,c);
    }
    for(int i=1;i<=n;i++) b[i]+=b[i-1];
    for(int i=1;i<=n;i++) cout<<b[i]<<" ";
    return 0;
}

二维差分

二维差分知识点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
798. 差分矩阵
   题目
   提交记录
   讨论
   题解
   视频讲解

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数 n,m,q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例：
2 3 4 1
4 3 4 1
2 2 2 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
using namespace std;
const int N=1e3+10;
int a[N][N],b[N][N],matrix[N][N];
int main()
{
    int n,m,q;
    cin>>n>>m>>q;
    ios::sync_with_stdio(false);
    for(int i=1;i<=n;i++) 
      for(int j=1;j<=m;j++)
         cin>>a[i][j];
    while(q--)
    {
        int x1,y1,x2,y2,c;
        cin>>x1>>y1>>x2>>y2>>c;
        b[x1][y1]+=c;//进行二维差分运算
        b[x2+1][y1]-=c;
        b[x1][y2+1]-=c;
        b[x2+1][y2+1]+=c;
    }
    for(int i=1;i<=n;i++)
      for(int j=1;j<=m;j++)
        matrix[i][j]=matrix[i-1][j]+matrix[i][j-1]+b[i][j]-matrix[i-1][j-1];/*算出全部子矩阵加减操作后的前缀和*/
    for(int i=1;i<=n;i++){
      for(int j=1;j<=m;j++)
      {
            cout<<a[i][j]+matrix[i][j]<<" ";/*将操作后的前缀和与原数组相加得到答案*/
      }
      cout<<endl;
    }
    return 0;
}

双指针算法

找双指针算法可以先写一个暴力的o(n^2)，然后找i和j是否满足单调性，如果满足就可以使用双指针算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
799. 最长连续不重复子序列
   题目
   提交记录
   讨论
   题解
   视频讲解

给定一个长度为 n 的整数序列，请找出最长的不包含重复的数的连续区间，输出它的长度。

输入格式
第一行包含整数 n。

第二行包含 n 个整数（均在 0∼105 范围内），表示整数序列。

输出格式
共一行，包含一个整数，表示最长的不包含重复的数的连续区间的长度。

数据范围
1≤n≤105
输入样例：
5
1 2 2 3 5
输出样例：
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
using namespace std;
const int N=1e5+10;
int a[N],s[N];
int main()
{
    ios::sync_with_stdio(false);
    int n;
    cin>>n;
    int res=0;
    for(int i=0;i<n;i++) cin>>a[i];
    for(int i=0,j=0;i<n;i++)
    {
        s[a[i]]++;//相当于选中当前当前这个数
        //为啥可以只查找A[i]是否重复，因为前面已经是连续不重复了，重复只能在a[i]
        while(s[a[i]]>1)//如果有重复，j开始查找，直到查找到没有没有数和a[i]重复为止
        {
            s[a[j]]--;//右移相当于当前这个选中状态被取消要减去1；
            j++;
        }
        res=max(res,i-j+1);
    }
    cout<<res<<endl;
    return 0;
}

链表的定义

链表是物理存储单元上非连续的、非顺序的存储结构，它是由一个个结点，通过指针来联系起来的，其中每个结点包括数据和指针。

屏幕截图 2022-01-06 160632

链表在内存中采用每个结点都分配在非连续的位置，结点与结点之间通过指针连在了一起，查找元素时需要遍历查找。

链表的表示

定义头节点：

由于链表的特点（查询或删除元素都要从头结点开始）,所以我们只要在链表中定义头结点即可(我学习采用的是头节点无数据型的链表表示)：

1577669607-4eeed00317fbd8a 
1
2
3
4
5
6
7
8
9
10
11
typedef struct Node{
    int data;
    struct Node* next;
}Node;//定义结构体，并创建结构体指针用来链接节点
Node* createList()
{
   Node* headNode;
   headNode=(Node*)malloc(sizeof(Node));
   headNode->next=NULL;
   return headNode;
}//创建结构体指针需要向内存申请空间，通常来说头节点初始化不指向任何节点

创建节点：

创建完头节点后我们需要创建新的节点用来存储数据：

1
2
3
4
5
6
7
8
Node* createNode(int data)
{
    Node* newNode;
    newNode=(Node*)malloc(sizeof(Node));
    newNode->data=data;
    newNode->next=NULL;
    return newNode;
}

连接节点：

链接节点可以采用两种方式：1. 头插法 2.尾插法

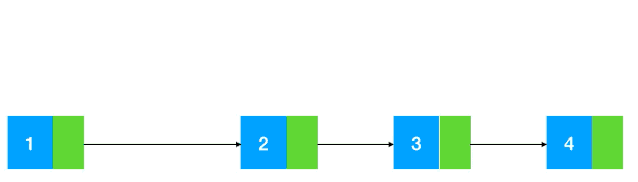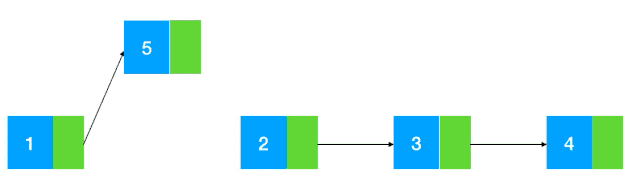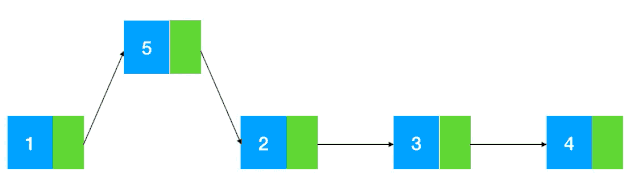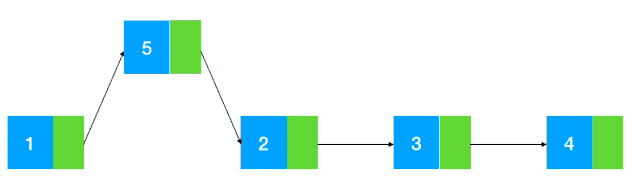
头插法：

1577669607-2500a8c3aad50ab

具体步骤如上图所示，将将前一个节点指向插入的节点，将插入的节点指向原下一个节点

1
2
3
4
5
6
7
void insertList(Node* headNode,int data)
{
    Node* newNode=createNode(data);
    newNode->next=headNode->next;
    headNode->next=newNode;
}//因为头插法需要头节点所以将头节点传入函数
//头插法最终输出时数据会逆向输出，因为前面的数据在链接后变到了最尾巴，输出时是顺序输出

尾插法（一）：

观察头插法会发现，插入节点时永远会在头节点插入，导致数据是逆序的。那么只要数据都是在链表的最后插入就不会有这个问题。尾插法在头插法的基础上，设置了一个单独的结构体指针保证结构体在插入时永远是在尾巴插入，这样数据存储就是顺序的。

这种尾插法有一个缺点，就是只能连续插入，不能分开插入，所以我们就有了第二种尾插法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Node* LinkList()
{
    Node* pMove;
    Node* headNode;
    headNode=pMove=(Node*)malloc(sizeof(Node));
    pMove->next=NULL;
    while(1)
    {
        int data;
        printf("请输入您的数据：");
        scanf("%d",&data);
        if(data==5) break;
        Node* newNode=createNode(data);
        pMove->next=newNode;
        pMove=newNode;
    }
    return headNode;
}//这里要创建headNode的原因是因为要先让headNode指向下一个节点不未NULL，要不然链表就断掉了。

尾插法（二）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int main()
{
   Node* headNode=createList();//建立头节点
   Node* tail=headNode;//建立一个指针用来插入节点
   //下面为测试节点
   LinkList(&tail,1);//结构体不包括地址，所以必须取地址符
   LinkList(&tail,2);
   LinkList(&tail,3);
   printList(headNode);
   return 0;
}
Node* LinkList(Node **ptail,int data)//实参引用结构题二级指针，来保证原函数tail能一直指向尾巴
{
    Node* newNode=createNode(data);
    (*ptail)->next=newNode;//这里要注意：*号的优先级比->低，所以必须用括号括起来
    (*ptail)=newNode;
    return (*ptail);//返回结构体指针
}

在任意位置插入节点

在任意处插入节点的重要点就在于要先找到要插入位置的地址，因为链表只能知道下一个节点，所以必须要遍历查找，并返回节点的地址，然后插入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Node* foundNode(Node* headNode,int searchdata)
{
    Node* pFound;
    int isFound=0;
    for(pFound=headNode->next;pFound;pFound=pFound->next)
    {
      if(pFound->data==searchdata){
          printf("找到了\n");
          isFound=1;
          return pFound;
      }
    }
    if(!isFound) printf("没找到\n");
    return NULL;
}
void insertNode(Node** pFound,int data)
{
   Node* newNode=createNode(data);
   newNode->next=(*pFound)->next;
   (*pFound)->next=newNode;
}
int main()
{
    Node* pFound;
    Node* headNode=createList();
    insertList(headNode,1);
    insertList(headNode,2);
    insertList(headNode,3);
    insertList(headNode,4);
    pFound=foundNode(headNode,2);
    insertNode(&pFound,6);
    printList(headNode);
    return 0;
}

打印链表

链表只能循环打印

1
2
3
4
5
6
7
8
9
10
11
void printList(Node* headNode)
{
   Node* pMove=headNode->next;
   printf("打印链表\n");
   while(pMove)
   {
      printf("%d->",pMove->data);
      pMove=pMove->next;
   }
   printf("NULL\n");
}

查找链表

查找链表我暂时只学到遍历查找，等后续学到了会更新

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void searchNode(Node* headNode,int searchdata)
{
    int isFound=0;
    Node* pMove=headNode->next;
    while(pMove)
    {
        if(pMove->data==searchdata)
        {
            printf("在此链表中找到了！\n");
            isFound=1;
            break;
        }
        pMove=pMove->next;
    }
    if(!isFound) printf("对不起没有找到！\n");
}

删除节点

一样的只会循环查找后删除，后续更新新的方法

删除节点有几个要注意的地方：

一：首先要定义两个指针，因为删除节点需要该节点的前节点链接到该节点的下一个节点，而单链表只能知道下一个节点，所以必须要两个指针来删除

二：就是要注意，当删除的节点是头节点，那么就必须特殊对待，直接将headNode指向删掉节点的下一个节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void deleteNode(Node* headNode,int deletenumber)
{
    Node *q,*p;
    int isFound=0;
    for(q=NULL,p=headNode->next;p;q=p,p=p->next)
    {
        if(p->data==deletenumber)//找到该节点
        {
            isFound=1;
            if(!q)//如果发现前节点是空，说明是头节点，那么只需要headNode指向p->next
                headNode=p->next;
            else
                q->next=p->next;
            free(p);
            break;
        }
    }
    if(!isFound) printf("未删除成功\n");
    else printf("删除成功\n");
}

静态链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
using namespace std;
const int N=1e5;
int val[N],ne[N],head[N],idx;
void init()
{
    head=-1;
    idx=0;
}
//插头
void add-to-head(int x)
{
    e[idx]=x;
    ne[idx]=head;
    head=idx;
    idx++;
}
//插到下标为k的地方
void add(int pos,int x)
{
    e[idx]=x;
    ne[idx]=ne[pos];
    ne[pos]=idx;
    idx++;
}
//删除下标为k的后面的结点
void remove(int pos)
{
    ne[k]=ne[ne[k]];
}
int main()
{
    init();
    
    return 0;
}

826. 单链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

   题目
   提交记录
   讨论
   题解
   视频讲解

实现一个单链表，链表初始为空，支持三种操作：

向链表头插入一个数；
删除第 k 个插入的数后面的数；
在第 k 个插入的数后插入一个数。
现在要对该链表进行 M 次操作，进行完所有操作后，从头到尾输出整个链表。

注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数，则按照插入的时间顺序，这 n 个数依次为：第 1 个插入的数，第 2 个插入的数，…第 n 个插入的数。

输入格式
第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令可能为以下几种：

H x，表示向链表头插入一个数 x。
D k，表示删除第 k 个插入的数后面的数（当 k 为 0 时，表示删除头结点）。
I k x，表示在第 k 个插入的数后面插入一个数 x（此操作中 k 均大于 0）。
输出格式
共一行，将整个链表从头到尾输出。

数据范围
1≤M≤100000
所有操作保证合法。

输入样例：
10
H 9
I 1 1
D 1
D 0
H 6
I 3 6
I 4 5
I 4 5
I 3 4
D 6
输出样例：
6 4 6 5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1e5+10;
int val[N],ne[N],head,idx;
void init()
{
    head=-1;
    idx=0;
}
void add_to_head(int x){
    val[idx]=x;
    ne[idx]=head;
    head=idx;
    idx++;
}

void deletex(int k)
{
    ne[k]=ne[ne[k]];
}

void add(int k,int x)
{
    val[idx]=x;
    ne[idx]=ne[k];
    ne[k]=idx;
    idx++;
}

int main()
{
    ios::sync_with_stdio(false);
    init();
    char oper;
    int n,x,k;
    cin>>n;
    while(n--)
    {
        cin>>oper;
        if(oper=='H'){
            cin>>x;
            add_to_head(x);
        }
        else if(oper=='I'){
            cin>>k>>x;
            add(k-1,x);//减一和上面原理一样
        }
        else {
            cin>>x;
            if(x==0) head=ne[head];//删去首节点也好理解，就是修改head最开始指向为原head指向的下一个指向
            deletex(x-1);//为什么要减去一，因为idx是从0开始，而k是从1开始，删除第k个插入的数，就相当于
            //在程序中删除第x-1个数
        }
    }
    int index=head;
    while(index!=-1)
    {
        cout<<val[index]<<" ";
        index=ne[index];
    }
    return 0;
}

##　双链表

双链表具体详解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
827. 双链表
   题目
   提交记录
   讨论
   题解
   视频讲解

实现一个双链表，双链表初始为空，支持 5 种操作：

在最左侧插入一个数；
在最右侧插入一个数；
将第 k 个插入的数删除；
在第 k 个插入的数左侧插入一个数；
在第 k 个插入的数右侧插入一个数
现在要对该链表进行 M 次操作，进行完所有操作后，从左到右输出整个链表。

注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数，则按照插入的时间顺序，这 n 个数依次为：第 1 个插入的数，第 2 个插入的数，…第 n 个插入的数。

输入格式
第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令可能为以下几种：

L x，表示在链表的最左端插入数 x。
R x，表示在链表的最右端插入数 x。
D k，表示将第 k 个插入的数删除。
IL k x，表示在第 k 个插入的数左侧插入一个数。
IR k x，表示在第 k 个插入的数右侧插入一个数。
输出格式
共一行，将整个链表从左到右输出。

数据范围
1≤M≤100000
所有操作保证合法。

输入样例：
10
R 7
D 1
L 3
IL 2 10
D 3
IL 2 7
L 8
R 9
IL 4 7
IR 2 2
输出样例：
8 7 7 3 2 9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
//这里填你的代码^^
#include <iostream>
#include <string>
using namespace std;
const int N=1e5+10;
int val[N],l[N],r[N],idx;
void insert(int k,int x)
{
    val[idx]=x;
    l[idx]=k;
    r[idx]=r[k];
    l[r[k]]=idx;
    r[k]=idx;
    idx++;
}
void init()
{
    r[0]=1;//下标为0一定为头指针
    l[1]=0;//下标为1一定为尾指针
    idx=2;
}
void remove(int k)
{
    r[l[k]]=r[k];
    l[r[k]]=l[k];
}
int main()
{
    init();
    int n;
    cin>>n;
    while(n--)
    {
        string oper;
        int k,x;
        cin>>oper;
        if(oper=="L")
        {
            cin>>x;
            insert(0,x);
        }
        else if(oper=="R")
        {
          cin>>x;
          insert(l[1],x);//因为add函数是向右插，所以向左移动一位然后在该地插入，就相当于在原来的左边插入
        }
        else if(oper=="IL")
        {
            cin>>k>>x;
            insert(l[k+1],x);
        }
        else if(oper=="IR")
        {
            cin>>k>>x;
            insert(k+1,x);//因为idx从2开始，而k从1开始，所以要加一
            //这里不用r[k+1]的原因是add函数是从k的右边插入，而k下标就对应了插入的k个数
        }
        else{
            cin>>k;
            remove(k+1);
        }
    }
    int cnt=r[0];
    while(cnt!=1)
    {
        cout<<val[cnt]<<" ";
        cnt=r[cnt];
    }
    return 0;
}
//注意代码要放在两组三个点之间，才可以正确显示代码高亮哦~

栈和单调栈

表达式求值（栈的应用）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
828. 模拟栈
   题目
   提交记录
   讨论
   题解
   视频讲解

实现一个栈，栈初始为空，支持四种操作：

push x – 向栈顶插入一个数 x；
pop – 从栈顶弹出一个数；
empty – 判断栈是否为空；
query – 查询栈顶元素。
现在要对栈进行 M 个操作，其中的每个操作 3 和操作 4 都要输出相应的结果。

输入格式
第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式
对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。

其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示栈顶元素的值。

数据范围
1≤M≤100000,
1≤x≤109
所有操作保证合法。

输入样例：
10
push 5
query
push 6
pop
query
pop
empty
push 4
query
empty
输出样例：
5
5
YES
4
NO
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <stack>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <cctype>
using namespace std;
stack<int> num;
stack<int> op;
void eval()
{
    int ans=0;
    int b=num.top();num.pop();
    int a=num.top();num.pop();
    char operation=op.top();op.pop();
    if(operation=='+') ans=a+b;
    if(operation=='-') ans=a-b;
    if(operation=='*') ans=a*b;
    if(operation=='/') ans=a/b;
    num.push(ans);
}
int main()
{
    unordered_map<char,int> h={{'+',1},{'-',1},{'*',2},{'/',2}};
    string s;
    cin>>s;
    for(int i=0;i<s.size();i++)
    {
        if(isdigit(s[i])){
            int j=i,a=0;
            while(j<s.size()&&isdigit(s[j]))
            {
                a=a*10+s[j]-'0';
                j++;
            }
            num.push(a);
            i=j-1;
        }
        else if(s[i]=='(') op.push(s[i]);
        else if(s[i]==')')
        {
            while(op.top()!='(') eval();
            op.pop();
        }
        else{
            while(op.size()&&h[op.top()]>=h[s[i]]) eval();
            op.push(s[i]);
        }
    }
    while(op.size()) eval();
    cout<<num.top()<<endl;
    return 0;
}

模拟队列和单调队列

模拟队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
实现一个队列，队列初始为空，支持四种操作：

push x – 向队尾插入一个数 x；
pop – 从队头弹出一个数；
empty – 判断队列是否为空；
query – 查询队头元素。
现在要对队列进行 M 个操作，其中的每个操作 3 和操作 4 都要输出相应的结果。

输入格式
第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式
对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。

其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示队头元素的值。

数据范围
1≤M≤100000,
1≤x≤109,
所有操作保证合法。

输入样例：
10
push 6
empty
query
pop
empty
push 3
push 4
pop
query
push 6
输出样例：
NO
6
YES
4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <string>
using namespace std;
const int N=1e5+10;
int queue[N],head,tt=-1;//初始化队列尾把为-1，这样插入的时候头和尾就会一样了
void push(int x)
{
    queue[++tt]=x;
}
void pop()
{
    head++;
}
int empty()
{
    if(head<=tt) return 0;
    else return 1;
}
int query()
{
    return queue[head];
}
int main()
{
    string operation;
    int n;
    cin>>n;
    while(n--)
    {
        cin>>operation;
        if(operation=="push")
        {
            int x;
            cin>>x;
            push(x);
        }
        if(operation=="pop")
        {
            pop();
        }
        if(operation=="empty")
        {
            if(!empty()) cout<<"NO"<<endl;
            else cout<<"YES"<<endl;
        }
        if(operation=="query")
        {
            cout<<query()<<endl;
        }
    }
    return 0;
}

单调队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
154. 滑动窗口
   题目
   提交记录
   讨论
   题解
   视频讲解

给定一个大小为 n≤106 的数组。

有一个大小为 k 的滑动窗口，它从数组的最左边移动到最右边。

你只能在窗口中看到 k 个数字。

每次滑动窗口向右移动一个位置。

以下是一个例子：

该数组为 [1 3 -1 -3 5 3 6 7]，k 为 3。

窗口位置	最小值	最大值
[1 3 -1] -3 5 3 6 7	-1	3
1 [3 -1 -3] 5 3 6 7	-3	3
1 3 [-1 -3 5] 3 6 7	-3	5
1 3 -1 [-3 5 3] 6 7	-3	5
1 3 -1 -3 [5 3 6] 7	3	6
1 3 -1 -3 5 [3 6 7]	3	7
你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式
输入包含两行。

第一行包含两个整数 n 和 k，分别代表数组长度和滑动窗口的长度。

第二行有 n 个整数，代表数组的具体数值。

同行数据之间用空格隔开。

输出格式
输出包含两个。

第一行输出，从左至右，每个位置滑动窗口中的最小值。

第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例：
8 3
1 3 -1 -3 5 3 6 7
输出样例：
-1 -3 -3 -3 3 3
3 3 5 5 6 7

思路：

最小值和最大值分开来做，两个for循环完全类似，都做以下四步：

  1. 解决队首已经出窗口的问题;
  2. 解决队尾与当前元素a[i]不满足单调性的问题;
  3. 将当前元素下标加入队尾;
  4. 如果满足条件则输出结果;

需要注意的细节：

  1. 上面四个步骤中一定要先3后4，因为有可能输出的正是新加入的那个元素
  2. 队列中存的是原数组的下标，取值时要再套一层，a[q[]];
  3. 算最大值前注意将hh和tt重置;
  4. 此题用cout会超时，只能用printf;
  5. hh从0开始，数组下标也要从0开始。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>
#include <string>
using namespace std;
const int N=1e6+10;
int hh,tt=-1,a[N],q[N];
int main()
{
    int n,k;
    cin>>n>>k;
    for(int i=0;i<n;i++) cin>>a[i];
    for(int i=0;i<n;i++)
    {
        if(hh<=tt&&k<i-q[hh]+1)  hh++;//维护窗口长度
        while(hh<=tt&&a[q[tt]]>=a[i]) tt--; //使队列单调
        q[++tt]=i;//传入最后一个满足的值
        if(i>=k-1) cout<<a[q[hh]]<<" ";
    }
    cout<<endl;
    hh=0,tt=-1;
    for(int i=0;i<n;i++){
        if(hh<=tt&&k<i-q[hh]+1) hh++;
        while(hh<=tt&&a[q[tt]]<=a[i]) tt--;
        q[++tt]=i;
        if(i>=k-1) cout<<a[q[hh]]<<" ";
    }
    return 0;
}

堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <iostream>
#include <string>
using namespace std;
const int N=1e5+10;
int h[N],hp[N],ph[N],cur_size,m;
void heap_swap(int a,int b)
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a],hp[b]);
    swap(h[a],h[b]);
}
void up(int x)
{
    while(x/2&&h[x/2]>h[x])
    {
       heap_swap(x,x/2);
        x>>=1;
    }
}
void down(int x)
{
    int t=x;
    if(x*2<=cur_size&&h[2*x]<h[t]) t=2*x;
    if(x*2+1<=cur_size&&h[2*x+1]<h[t]) t=2*x+1;
    if(x!=t)
    {
        heap_swap(t,x);
        down(t);
    }
}
int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        string op;
        cin>>op;
        if(op=="I")
        {
            int x;
            cin>>x;
            cur_size++;
            m++;
            ph[m]=cur_size,hp[cur_size]=m;
            h[cur_size]=x;
            up(cur_size);//最后插入，需要up
        }
        else if(op=="PM") cout<<h[1]<<endl;
        else if(op=="DM")
        {
            heap_swap(1,cur_size);
            cur_size--;
            down(1);
        }
        else if(op=="D")
        {
            int x;
            cin>>x;
            int k=ph[x];//找到第k个插入的数在堆中的位置，因为删除k后，我们就丢失额了原先第k个数的位置
            heap_swap(ph[x],cur_size);
            cur_size--;
            down(k);
            up(k);
        }
        else{
            int k,x;
            cin>>k>>x;
            h[ph[k]]=x;
            down(ph[k]);
            up(ph[k]);
        }
    }
    return 0;
}
//注意代码要放在两组三个点之间，才可以正确显示代码高亮哦~

KMP

KMP全称为Knuth Morris Pratt算法，三个单词分别是三个作者的名字。KMP是一种高效的字符串匹配算法，用来在主字符串中查找模式字符串的位置(比如在“hello,world”主串中查找“world”模式串的位置)。

KMP算法的高效体现在哪

高效性是通过和其他字符串搜索算法对比得到的，在这里拿BF(Brute Force)算法做一下对比。BF算法是一种最朴素的暴力搜索算法。它的思想是在主串的[0, n-m]区间内依次截取长度为m的子串，看子串是否和模式串一样(n是主串的长度，m是子串的长度)。 BF的时间复杂度是O(N*N)，存在很大优化空间。当模式串和主串匹配时，遇到模式串中某个字符不能匹配的情况，对于模式串中已经匹配过的那些字符，如果我们能找到一些规律，将模式串多往后移动几位，而不是像BF算法一样，每次把模式串移动一位，就可以提高算法的效率。比如说在“ababaababacd”中查找“ababac”，可以避免一些字符之间的比较。

下面通过一个具体的例子来看看可以跳过的情况。比如主模式串是”ababaeaba”,模式串是”ababacd”,在BF算法中，遇到不匹配的情况是这样处理的:

1
2
3
main:    "ababaeaba" // 例如这两个串，当sub为"ababaea"时和"ababacd"进行对
pattern: "ababacd"   // 比，当main[i]为e时，发现和pattern[j]的值e不一致，BF
                                         // 的做法是去下一个sub,即用"babaeab"和pattern进行比较。

我没希望找到一些规律，遇到两个字符不匹配的情况时，希望可以多跳几个字符，减少比较次数。KMP算法的思想是：在模式串和主串匹配过程中，当遇到不匹配的字符时，对于主串和模式串中已对比过相同的前缀字符串，找到长度最长的相等前缀串，从而将模式串一次性滑动多位，并省略一些比较过程。在上个例子，KMP算法中，是这样处理的：

1
2
3
4
5
6
7
8
9
10
11
12
13
main:    "ababaeaba" // 比如main中的"ababa"子串，对标为[2~4]的"aba"和pattern中下
pattern: "ababacd"   // 标为[0~2]的"aba"相同,此时可以滑动j-k位,即j=j-k。(其中j是
                                         // pattern中"c"的下标,k是"abc"的长度)。
            "ababaeaba"      // 比较过程中，main[5]为"e"和pattern[5]为"c"不匹配，但是两个
            "ababacd"            // 串中都有相同的"aba"前缀,所以可以滑动j-k位
                    |           
                    ∨
            "ababaeaba"   
                "ababacd"
                    |               // 滑动j-k位后发现main[5]和patterb[3]不相同，需要再次滑动
                    ∨
            "ababaeaba"   
                    "ababacd" // 滑动过程和上次类似。

通过这个例子可以看出，每次滑动的位数是j-k，滑动位数和主串无关，仅通过模式串就可以求出。在KMP算法中通过next数组来存储当两个字符不相等时模式串应该移动的位数。

如何KMP算法的next数组 再次明确next数组的含义 : next数组用来存模式串中每个前缀最长的能匹配前缀子串的结尾字符的下标。 next[i] = j 表示下标以i-j为起点，i为终点的后缀和下标以0为起点，j为终点的前缀相等，且此字符串的长度最长。用符号表示为p[0~j] == p[i-j~i]。下面以”ababacd”模式串为例，给出这个串的next数组。

模式前缀 前缀结尾下标 最长能匹配前缀子串结尾字符的下标 next数组的取值 匹配情况
a 0 -1 next[0] = -1 无
ab 1 -1 next[1] = -1 无
aba 2 0 next[2]=0 pattern[2]==pattern[0]
abab 3 1 next[3]=1 pattern[2:4]==pattern[0:2]
ababa 4 2 next[4]=2 pattern[2:5]==pattern[0:3]
ababac 5 -1 next[5]=-1 无

KMP的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
const int N=100010,M=1000010;
int n,m,ne[N];
char p[N],s[M];
int main()
{
    cin>>n>>p+1>>m>>s+1;//kmp算法通常都是以下标为1开始

    //j从下标零开始,是因为我们要判断的是p[j+1]是否等于p[i]，如果是p[j]与p[i]比较，那么当
    //p[j]与p[i]不匹配的时候,就找不到最长的前后缀匹配和了
    for(int i=2,j=0;i<=n;i++)//因为p的第一个ne[1]=0的，所以从第二个开始
    {
        while(j&&p[i]!=p[j+1]) j=ne[j];
        if(p[i]==p[j+1]) j++;
        ne[i]=j;
    }

    //kmp匹配
    for(int i=1,j=0;i<=m;i++)
    {
        while(j&&s[i]!=p[j+1]) j=ne[j];
        if(s[i]==p[j+1]) j++;
        if(j==n)
        {
            cout<<i-n<<" ";
        }
    } 
    return 0;
}

Trie

哈希表

拉链法

https://cdn.acwing.com/media/article/image/2021/01/17/2675_9b33804c58-4.jpg 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>
#include <cstring>
using namespace std;
const int N=1e5+3;
int h[N],ne[N],e[N],idx,n;
void insert(int x)
{
    int k=(x%N+N)%N;
    //为什么x%N后还要加N，因为在c++中-10mod3=-1，所以要把负数映射到正数
    e[idx]=x;//单链表求法
    ne[idx]=h[k];
    h[k]=idx++;
}
bool query(int x)
{
    bool flag=false;
    int k=(x%N+N)%N;
    for(int i=h[k];i!=-1;i=ne[i])
    {
        if(e[i]==x){//找到后就可以返回查询结果
            flag=true;
            break;
        }
    }
    return flag;
}
int main()
{
    memset(h,-1,sizeof h);
    cin>>n;
    while(n--)
    {
        int x;
        string op;
        cin>>op>>x;
        if(op=="I") insert(x);
        else{
            if(query(x)) cout<<"Yes"<<endl;
            else cout<<"No"<<endl;
        }
    }
    return 0;
}

开放寻址法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
#include <cstring>
using namespace std;
const int N=200003,null=0x3f3f3f3f;//通常要比询问次数的范围大2-3倍，同时还是质数
//0x3f3f3f3f可以作为无穷大来比较
int h[N],n;
int find(int x)
{
    int k=(x%N+N)%N;
    while(h[k]!=null&&h[k]!=x)
    {
        k++;
        if(k==N) k=0;
    }
    return k;
}
int main()
{
    memset(h,0x3f,sizeof h);
    cin>>n;
    while(n--)
    {
        string op;
        int x;
        cin>>op>>x;
        if(op=="I")
        {
            int k=find(x);
            h[k]=x;
        }
        else{
            if(h[find(x)]==null) cout<<"No"<<endl;
            else cout<<"Yes"<<endl;
        }
    }
    return 0; 
}

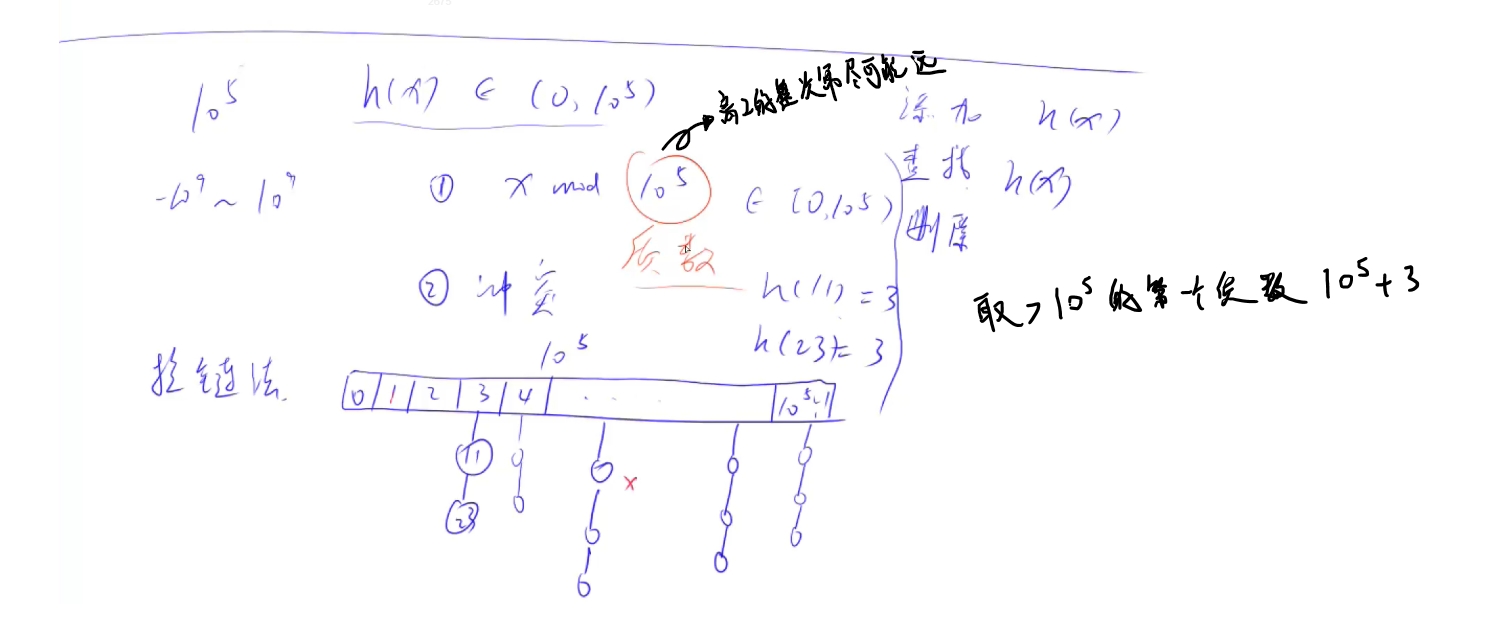
字符串哈希表

(字符串哈希) O(n)+O(m) 全称字符串前缀哈希法，把字符串变成一个p进制数字（哈希值），实现不同的字符串映射到不同的数字。 对形如 X1X2X3⋯Xn−1Xn的字符串,采用字符的ascii 码乘上 P 的次方来计算哈希值。

映射公式 (X1×Pn−1+X2×Pn−2+⋯+Xn−1×P1+Xn×P0)modQ 注意点：

  1. 任意字符不可以映射成0，否则会出现不同的字符串都映射成0的情况，比如A,AA,AAA皆为0
  2. 冲突问题：通过巧妙设置P (131 或 13331) , Q (264)(264)的值，一般可以理解为不产生冲突。

问题是比较不同区间的子串是否相同，就转化为对应的哈希值是否相同。 求一个字符串的哈希值就相当于求前缀和，求一个字符串的子串哈希值就相当于求部分和。

前缀和公式 h[i+1]=h[i]×P+s[i]h[i+1]=h[i]×P+s[i] i∈[0,n−1]i∈[0,n−1] h为前缀和数组，s为字符串数组 区间和公式 h[l,r]=h[r]−h[l−1]×Pr−l+1h[l,r]=h[r]−h[l−1]×Pr−l+1 区间和公式的理解: ABCDE 与 ABC 的前三个字符值是一样，只差两位， 乘上 P2P2 把 ABC 变为 ABC00，再用 ABCDE - ABC00 得到 DE 的哈希值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
#include <cstring>
using namespace std;
typedef unsigned long long ull;
const int N=1e5+10,P=131;
char str[N];
ull p[N],h[N];
int get_val(int l, int r)
{
    return h[r]-h[l-1]*p[r-l+1];
    //利用求区间和的思想，但是h[l-1]位次比h[r]低，所以需要将h[l-1]左移
    //比如h[l-1]=AB,h[r]=ABCD,那么h[l-1]*p[r-l+1]就相当于ABCD-AB00=CD
}
int main()
{
    int n,m;
    cin>>n>>m;
    scanf("%s",str+1);
    p[0]=1;
    for(int i=1;i<=n;i++)
    {
        p[i]=p[i-1]*P;//求出每项的系数是多少
        h[i]=h[i-1]*P+str[i];//前缀和思想这个可以理解成2*5^n-1+3*5^n-2……
    }
    while(m--)
    {
        int l1,r1,l2,r2;
        cin>>l1>>r1>>l2>>r2;
        //判断两个字符串的哈希值是否相同，如果相同代表字符串完全相同
        if(get_val(l1,r1)==get_val(l2,r2)) cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}

在计算最短路时，Dijkstra算法不能处理带有负权的图，bellman_ford和spfa可以处理带有负权边的图，spfa是对bellman_ford的优化。

图论

Dijkstra算法

在Dijkstra算法中，稠密图使用邻接矩阵，稀疏图使用邻接表

朴素Dijkstra算法

在使用Dijkstra算法时，如果有向图中出现重边或者是有环的话，只采用代价最小的边

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
给定一个 n个点 m条边的有向图，图中可能存在重边和自环，所有边权均为正值。
请你求出 1号点到 n号点的最短距离，如果无法从 1号点走到 n号点，则输出 −1。

输入格式
第一行包含整数 n和 m。
接下来 m行每行包含三个整数 x,y,z，表示存在一条从点 x到点 y的有向边，边长为 z。

输出格式
输出一个整数，表示 1号点到 n号点的最短距离。
如果路径不存在，则输出 −1。

数据范围
1≤n≤500,
1≤m≤105,
图中涉及边长均不超过10000。

输入样例：
3 3
1 2 2
2 3 1
1 3 4
输出样例：
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N=510;
int n,m,g[N][N],dist[N];
bool st[N];
int dijkstra()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    for(int i=1;i<=n;i++){
        int t=-1;
        for(int j=1;j<=n;j++)
            if(!st[j]&&(t==-1||dist[t]>dist[j]))
                t=j;
        st[t]=true;
        for(int j=1;j<=n;j++)
            dist[j]=min(dist[j],dist[t]+g[t][j]);
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    else return dist[n];
}
int main()
{
    cin>>n>>m;
    memset(g,0x3f,sizeof g);
    while(m--)
    {
        int a,b,c;
        cin>>a>>b>>c;
        g[a][b]=min(g[a][b],c);
    }
    int t = dijkstra();
    cout<<t<<endl;
    return 0;
}

堆优化Dijkstra算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
给定一个 n个点 m条边的有向图，图中可能存在重边和自环，所有边权均为非负值。
请你求出 1号点到 n号点的最短距离，如果无法从 1号点走到 n号点，则输出 −1。

输入格式
第一行包含整数 n和 m。
接下来 m行每行包含三个整数 x,y,z，表示存在一条从点 x到点 y的有向边，边长为 z。

输出格式
输出一个整数，表示 1号点到 n号点的最短距离。如果路径不存在，则输出 −1。

数据范围
1≤n,m≤1.5×105,
图中涉及边长均不小于 0，且不超过 10000。数据保证：如果最短路存在，则最短路的长度不超过 109。

输入样例：
3 3
1 2 2
2 3 1
1 3 4
输出样例：
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N=2e5;
int h[N],n,m,ne[N],val[N],idx,w[N],dist[N];
bool state[N];
typedef pair<int,int> PII;
void add(int a,int b,int c)
{
    val[idx]=b;
    w[idx]=c;
    ne[idx]=h[a];
    h[a]=idx++;
}
int dijkstra()
{
    memset(dist,0x3f,sizeof dist);//默认将dist置为最大
    dist[1]=0;//将第一个点置为0
    priority_queue<PII,vector<PII>,greater<PII>>q;//设置堆
    q.push({0,1});
    while(q.size())//堆不为空就循环
    {
        auto t = q.top();//取出堆首元素
        q.pop();
        int ver = t.second,distance = t.first;
        if(state[ver]) continue;//如果访问到已经最优的结点就进行下次循环
        state[ver]=true;
        for(int i=h[ver];i!=-1;i=ne[i])//循环每一条可以访问的边
        {
            int j=val[i];
            if(dist[j]>dist[ver]+w[i]){ // 如果满足更新条件就更新
                dist[j]=dist[ver]+w[i];
                q.push({dist[j],j});
            }
        }
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    else return dist[n];
}
int main()
{
    memset(h,-1,sizeof h);
    cin>>n>>m;
    while(m--)
    {
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
    }
    auto t=dijkstra();
    cout<<t<<endl;
    return 0;
}

bellman_ford

Bellman-ford 算法是求含负权图的单源最短路径的一种算法，效率较低，代码难度较小。其原理为连续进行松弛，在每次松弛时把每条边都更新一下，若在 n-1 次松弛后还能更新，则说明图中有负环，因此无法得出结果，否则就完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
给定一个 n个点 m条边的有向图，图中可能存在重边和自环， 边权可能为负数。
请你求出从 1号点到 n号点的最多经过 k条边的最短距离，如果无法从 1号点走到 n号点，输出 impossible。
注意：图中可能 存在负权回路 。

输入格式
第一行包含三个整数 n,m,k。
接下来 m行，每行包含三个整数 x,y,z，表示存在一条从点 x到点 y的有向边，边长为 z。
点的编号为 1∼n。

输出格式
输出一个整数，表示从 1号点到 n号点的最多经过 k条边的最短距离。
如果不存在满足条件的路径，则输出 impossible。

数据范围
1≤n,k≤500,
1≤m≤10000,
1≤x,y≤n，
任意边长的绝对值不超过 10000。

输入样例：
3 3 1
1 2 1
2 3 1
1 3 3
输出样例：
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=510,M=1e5+10;
int dist[N],backup[N],n,m,k;
struct edge
{
    int a,b,w;
}edge[M];
void bellman_ford()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    for(int i=0;i<k;i++)
    {
        memcpy(backup,dist,sizeof dist);
        for(int j=0;j<m;j++)
        {
            int a=edge[j].a,b=edge[j].b,w=edge[j].w;
            if(dist[b]>backup[a]+w)
                dist[b]=backup[a]+w;
        }
    }
}
int main()
{
    cin>>n>>m>>k;
    for(int i=0;i<m;i++)
    {
        int a,b,w;
        cin>>a>>b>>w;
        edge[i]={a,b,w};
    }
    bellman_ford();
    if(dist[n]>0x3f3f3f3f/2) cout<<"impossible"<<endl;
    //为啥是0x3f3f3f3f/2，因为当存在负权边的时候，每次更新dist都会变小，但我们还是认为他是正无穷
    else cout<<dist[n]<<endl;
    return 0;
}

spfa算法

Bellman_ford算法会遍历所有的边，但是有很多的边遍历了其实没有什么意义，我们只用遍历那些到源点距离变小的点所连接的边即可，只有当一个点的前驱结点更新了，该节点才会得到更新；因此考虑到这一点，我们将创建一个队列每一次加入距离被更新的结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
给定一个 n个点 m条边的有向图，图中可能存在重边和自环， 边权可能为负数。
请你求出 1号点到 n号点的最短距离，如果无法从 1号点走到 n号点，则输出 impossible。
数据保证不存在负权回路。

输入格式
第一行包含整数 n和 m。
接下来 m行每行包含三个整数 x,y,z，表示存在一条从点 x到点 y的有向边，边长为 z。

输出格式
输出一个整数，表示 1号点到 n号点的最短距离。
如果路径不存在，则输出 impossible。

数据范围
1≤n,m≤105,
图中涉及边长绝对值均不超过 10000。

输入样例：
3 3
1 2 5
2 3 -3
1 3 4
输出样例：
2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N=2e5;
int head[N],val[N],ne[N],w[N],idx,dist[N],n,m;
bool state[N];
void add(int a,int b,int c)
{
    val[idx]=b;
    w[idx]=c;
    ne[idx]=head[a];
    head[a]=idx++;
}
void spfa()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    queue<int> q;
    state[1]=true;//用来判断是否入队列
    q.push(1);
    while(q.size())
    {
        int t=q.front();
        q.pop();
        state[t]=false;//从队列取出后标记为假
        for(int i=head[t];i!=-1;i=ne[i])
        {
            int j = val[i];
            if(dist[j]>dist[t]+w[i]) // 如果边的权重更新，就将更新的点入栈
            {
                dist[j]=dist[t]+w[i];
                if(!state[j]){
                    q.push(j);
                    state[j]=true;
                }
            }
        }
    }
}
int main()
{
    memset(head,-1,sizeof head);
    cin>>n>>m;
    for(int i=0;i<m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
    }
    spfa();
    if(dist[n]==0x3f3f3f3f) cout<<"impossible"<<endl;
    else cout<<dist[n]<<endl;
    return 0;
}

树

先序创建二叉树

算法思想

先序创建二叉树采用递归的方式实现，先传入二叉树的根节点指针的地址，然后依次递归读入二叉树节点，当读入的是'@'时，将递归得到的根节点赋予NULL，当读入的不为'@'时，将该值赋值到根节点值，并依此递归左儿子和右儿子。

关键问题1:为什么要传入根节点的地址?

因为我们已知的是根节点指针，它指向malloc开辟的BiTree空间的首地址，当传入的是根节点指针而不是根节点指针的地址时，在函数中会copy一个该根节点指针指向的空间。但我们如果传入的是根节点指针的地址，函数内部不会重新copy一个空间。

其思想与函数传入实参和形参相似

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <algorithm>
#include <string>
#include "Traverser.cpp"
using namespace std;
typedef struct BiTree
{
    char data;
    struct BiTree *lchild,*rchild;
}BiTree;
void CreateBiTree(BiTree* &T)
{
    char ch;
    cin>>ch;
    if(ch=='@') T=NULL;
    else{
        T=(BiTree*)malloc(sizeof(BiTree));
        T->data=ch;
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    }
}
void PreOrderTraverser(BiTree* &T)
{
    if(T)
    {
        cout<<T->data<<" ";
        PreOrderTraverser(T->lchild);
        PreOrderTraverser(T->rchild);
    }
}
int main()
{
    BiTree* root;
    CreateBiTree(root);
    PreOrderTraverser(root);
    return 0;
}

遍历二叉树

代码部分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include <iostream>
#include <algorithm>
#include <string>
#include <stack>
#include <algorithm>
#include <string>
using namespace std;
typedef struct BiTree
{
    char data;
    struct BiTree *lchild,*rchild;
}BiTree;
void CreateBiTree(BiTree* &T)
{
    char ch;
    cin>>ch;
    if(ch=='@') T=NULL;
    else{
        T=(BiTree*)malloc(sizeof(BiTree));
        T->data=ch;
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    }
}

//递归实现
void PreOrderTraverser(BiTree *T)
{
    if(T)
    {
        cout<<T->data<<" ";
        PreOrderTraverser(T->lchild);
        PreOrderTraverser(T->rchild);
    }
}
void InOrderTraverser(BiTree *T)
{
    if(T)
    {
        InOrderTraverser(T->lchild);
        cout<<T->data<<" ";
        InOrderTraverser(T->rchild);
    }
}
void PostOrderTraverser(BiTree *T)
{
    if(T)
    {
        PostOrderTraverser(T->lchild);
        PostOrderTraverser(T->rchild);
        cout<<T->data<<" ";
    }
}


//非递归实现
void InOrderTraverser_2(BiTree* T)
{
    stack<BiTree*> op;
    BiTree* p=T;
    while(p||op.size())
    {
        if(p){
            op.push(p);
            p=p->lchild;
        }
        else{
            p=op.top();    
            op.pop();
            cout<<p->data<<" ";                                           
            p=p->rchild;
        }
    }
}
void PreOrderTraverser_2(BiTree* T)
{
    stack<BiTree*>op;
    BiTree* p=T;
    while(p||op.size())
    {
        if(p){
            cout<<p->data<<" ";
            op.push(p);
            p=p->lchild;
        }
        else{
            p=op.top();
            op.pop();
            p=p->rchild;
        }
    }
}


int main()
{
    BiTree* root;
    CreateBiTree(root);
    PreOrderTraverser(root);
    cout<<endl;
    PreOrderTraverser_2(root);
    cout<<endl;
    InOrderTraverser(root);
    cout<<endl;
    InOrderTraverser_2(root);
    cout<<endl;
    PostOrderTraverser(root);
    cout<<endl;
    return 0;
}

计算二叉树

代码部分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
typedef struct BiTree
{
    char data;
    struct BiTree *lchild,*rchild;
}BiTree;
void CreateBiTree(BiTree* &T)
{
    char ch;
    cin>>ch;
    if(ch=='@') T=NULL;
    else{
        T=(BiTree*)malloc(sizeof(BiTree));
        T->data=ch;
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    }
}
int BiTreeDepth(BiTree* T)
{
    if(!T) return 0;
    else{
        int m=BiTreeDepth(T->lchild);
        int n=BiTreeDepth(T->rchild);
        return m>n?(m+1):(n+1);
    }
}
int CountNode(BiTree* T)
{
    if(T==NULL) return 0;
    else return CountNode(T->lchild)+CountNode(T->rchild)+1;
}
int CountLeaves(BiTree* T)
{
    int cnt=0;
    if(T==NULL) return 0;
    if((!T->lchild)&&(!T->rchild))  cnt++;;
    int lcnt=CountLeaves(T->lchild);
    int rcnt=CountLeaves(T->rchild);
    cnt+=lcnt+rcnt;
    return cnt;
}
int main()
{
    BiTree *root;
    CreateBiTree(root);
    cout<<BiTreeDepth(root)<<endl;
    return 0;
}
#数据结构 #acwing #算法学习
算法学习
http://www.ooorz.site/2022/10/23/算法学习/
作者
Lin Xinjie
发布于
2022年10月23日
更新于
2024年10月21日
许可协议